Inhaltsverzeichnis
Lernpfad: GeoGebra - Grafik 3D
Räumliche Objekte werden in der Zeichenebene beispielsweise in Frontalansichten oder im Schrägriss dargestellt. GeoGebra - Grafik 3D bietet zahlreiche visuelle Werkzeuge, mit denen solche Objekte erzeugt und vermessen werden können:
Hinweis: Die Beta-Version der Software kann von der Webseite http://download.geogebra.org/installers/5.0/ für Linux, MacOS und Windows bezogen werden. Die Software wird häufig aktualisiert, beispielsweise sieht die Werkzeugleiste im August 2014 wie folgt aus:
Grundlegende Befehle
In der Eingabezeile werden 3-dimensionale Objekte wie für die Grafik-Ansicht eingetragen.
- Eingabe eines Punktes:
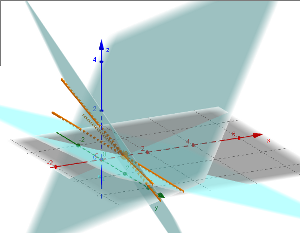
A := (1,4,-2) - Festlegen einer Geraden:
g := Gerade(A,B) - Festlegen einer Ebene:
e := Ebene(A,B,C) - Schnittmenge zweier Objekte:
S:=Schneide(g,e) - Kugel:
Kugel((0,0,0),4)
Hinweis: Oft lassen sich (vermutete) Eigenschaften und Abhängigkeiten von 3D-Objekten erst erkennen, wenn die Ansicht gewechselt wird - wähle daher auch die Frontalansicht oder drehe den Koordinatenausschnitt mit dem Drehe-Werkzeug …
Hinweis: Sobald ein freier Punkt in der 3D-Ansicht fokussiert wird kann dieser entweder horizontal  oder vertikal
oder vertikal  verschoben werden. Der Mausklick auf den Punkt schaltet zwischen diesen beiden Varianten um.
verschoben werden. Der Mausklick auf den Punkt schaltet zwischen diesen beiden Varianten um.
Analytische Geometrie des Raumes
In der 6. Klasse untersuchen wir die Lage von Punkten, Geraden und Ebenen im Raum und ihre Lagebeziehungen. Ebene Flächen begrenzen einfache Körper wie Prismen und Pyramiden.
Spezialthemen:
- Symmetrieebene zweier Ebenen („Winkelhalbierende“)
Kurven und Flächen im Raum
Flächen f(u,v) in Parameterdarstellung werden als Spuren von Parameterkurven f(u) dargestellt, die über den Parameter v animiert werden …
Anwendungen der Integralrechnung
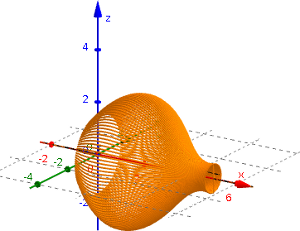 Rotationskörper entstehen, wenn sich Kurven um 360° um eine Achse drehen. Diese Drehung kann in der GeoGebra Grafik 3D-Ansicht mit dem GeoGebra-Befehl
Rotationskörper entstehen, wenn sich Kurven um 360° um eine Achse drehen. Diese Drehung kann in der GeoGebra Grafik 3D-Ansicht mit dem GeoGebra-Befehl Drehe(<Kurve>,<Winkel>,<Achse>) dargestellt werden.
Spezialthema: Polyeder
Spezialthema: Kurven als Schnitte zweier Flächen
Neben den Kegelschnittslinien betrachten wir weitere Schnitte zweier Flächen, z.B.:
Zurück zu Analytische Geometrie des Raumes | Kurven und Flächen im Raum | Anwendungen der Integralrechnung