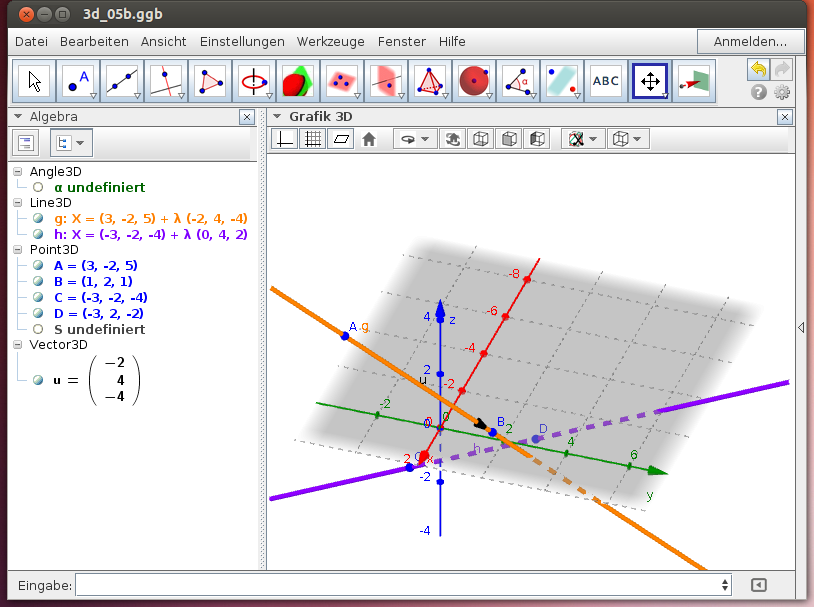
Lagebeziehungen zwischen Geraden im Raum: Windschiefe Geraden
Geraden können im Raum
- identisch sein: g = h
- parallel sein: g || h
- einander schneiden: g ∩ h = {S}
- windschief sein: g ∩ h = {}, g nicht parallel zu h
Beispiel:
Untersuche die Lagebziehung der beiden Geraden g[A(3|-2|5), B(1|2|1)] und h[C(-3|-2|4), D(-3|2|-2)]!
Aufgaben:
- Drehe die Darstellung der beiden Geraden g und h mit dem Drehe-Werkzeug und beschreibe die Lage der windschiefen Geraden g und h!
- Vergleiche mit schneidenden Geraden!
Zurück zu Analytische Geometrie des Raumes