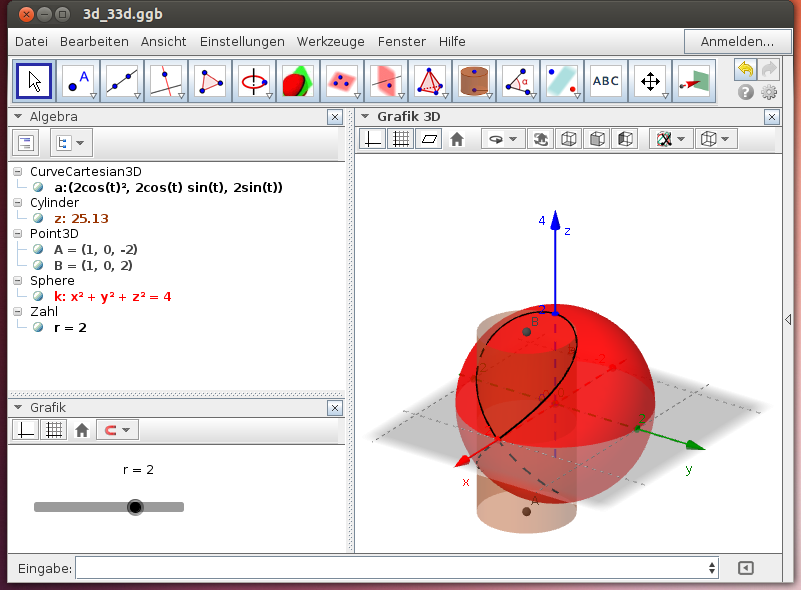
Die Viviani-Kurve

tm.jpg 7, S. 193

Beschreibe die Eigenschaften der Kurve tex:X(t) = (r \cdot (\cos (t))^2}, r \cdot \cos (t) \cdot \sin (t), r \cdot \sin (t)) für tex:t \in [0; 2 n \pi]:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Stelle die Zylinderfläche z und die Kugelfläche k im obigen GeoGebra-Beispiel sichtbar und unsichtbar und beobachte, dass die Viviani-Kurve auf beiden Flächen liegt! Begründe, dass die Viviani-Kurve dem Schnitt der Mittelpunktskugel mit Radius r mit dem Kreiszylinder mit Radius r/2, dessen Achse durch den Punkt (r/2|0|0) verläuft, entspricht!
  • Vergleiche mit der Darstellung der Viviani-Kurve und ihren Projektionen auf die Koordinatenebenen!

Zurück zu Kurven und Flächen im Raum


Zuletzt angesehen: • 3d_31c • 3d_33a • 3d_33b • 3d_33c • 3d_33d