Das vektorielle Produkt

tm.jpg 6, S. 106 - 107

Das vektorielle Produkt (Kreuzprodukt) zweier Vektoren tex:\vec a und tex:\vec b ergibt im Raum einen Normalvektor zu tex:\vec a und tex:\vec b.

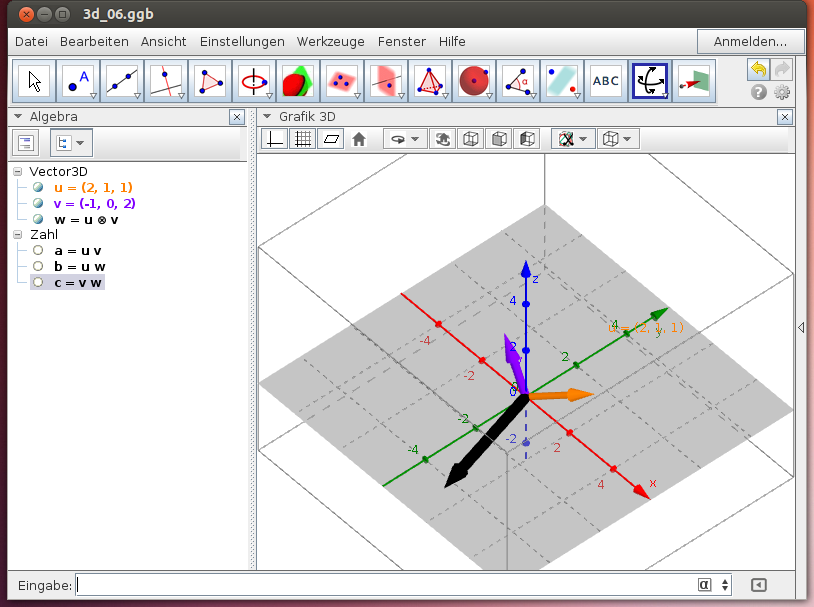
Hinweis: Berechne das vektorielle Produkt in GeoGebra mit Hilfe des Symboles ⊗:

Beispiel:

Berechne den Normalvektor tex:\vec w zu den beiden Vektoren tex:\vec u = (2,1,1) und tex:\vec v = (-1,0,2)!

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Überprüfe mit dem Orthogonalitätskriterium, dass der Normalvektor tex:\vec w auf beide Vektoren tex:\vec u und tex:\vec v normal steht!
  • Überprüfe anhand der im obigen Beispiel gegebenen Vektoren, dass das Kreuzprodukt nicht kommutativ ist!
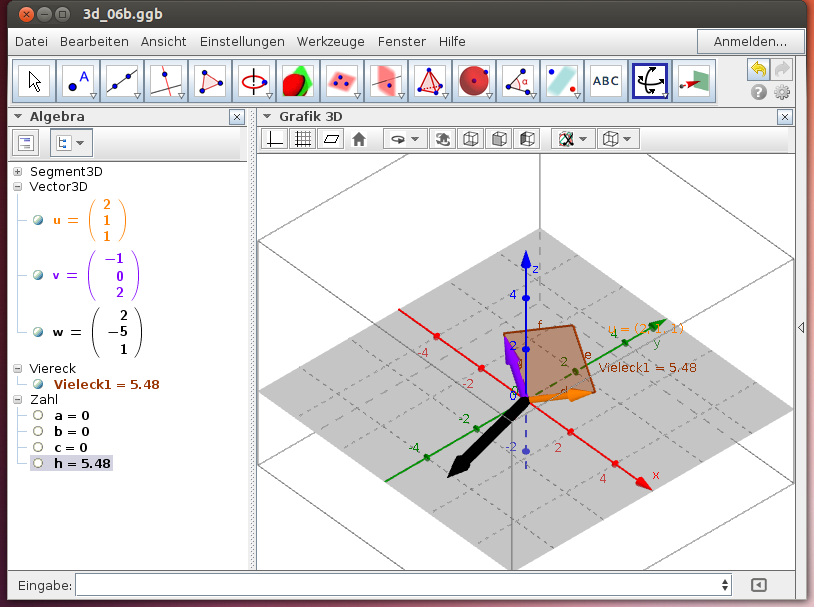
  • Rechne nach, dass gilt: Der Betrag des Normalvektors tex:|\vec w| ist gleich dem Flächeninhalt des von den beiden Vektoren tex:\vec u und tex:\vec v aufgespannten Parallelogramms.

Lösung:

Zurück zu Analytische Geometrie des Raumes


Zuletzt angesehen: • 3d_01 • 3d_03 • 3d_04 • 3d_06