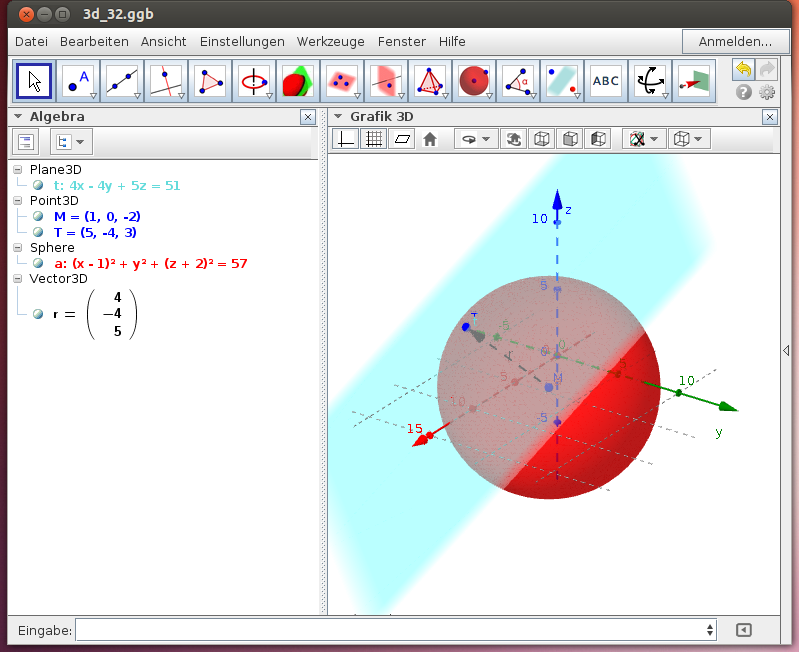
Tangentialebene an eine Kugel im gegebenen Berührungspunkt

7, S. 182 - 183

Beispiel: Bestimme die Gleichung der Tangentialebene im Punkt T(5|-4|3) der Kugel k: x² + y² + z² - 2x + 4z = 52!

GeoGebra stellt nach Eingabe der Kugelgleichung in der obigen Form die Gleichung mit vollständigen Quadraten dar, sodass die Koordinaten des Kugelmittelpunkts leicht abgelesen werden können. Lege den Mittelpunkt als Punkt fest und definiere den Radiusvektor ! Schließlich erhältst du die gesuchte Tangentialebene mit dem GeoGebra-Befehl Normalebene(<Punkt>, <Vektor>):

Download der GeoGebra-Datei

Ergebnis: Die gesuchte Tangentialebene hat die Gleichung t: 4x - 4y + 5z = 51

Zurück zu Kurven und Flächen im Raum