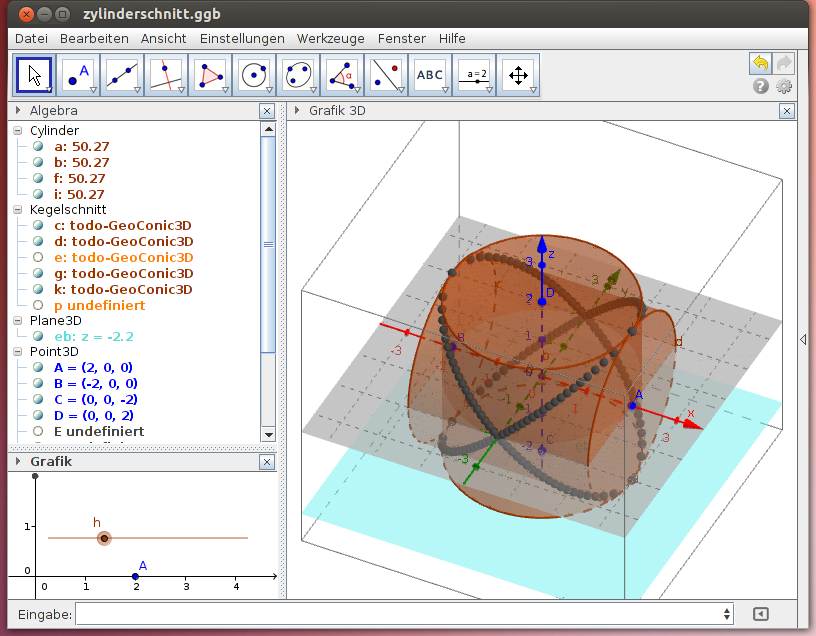
Durchdringung zweier Zylinder
Zwei Kreiszylinder mit gleichen Radien, deren Achsen einander in rechtem Winkel schneiden, durchdringen einander. Beobachte die Form der Schnittkurve im folgenden GeoGebra-Beispiel:
Hinweis: Beide Zylinder werden durch die Horinzontalebene geschnitten. Die Schnittpunkte der beiden Schnittkurven ergeben jeweils zwei Punkte der Schnittkurve. Die Animation des Schiebereglers h bewirkt die Parallelverschiebung der Ebene, sodass alle Schnittkurven dargestellt werden.
Aufgaben:
- Starte die Animation des Schiebereglers für h und stelle die Schnittkurve als Punktespur der Schnittpunkte beider Schnittkurven dar!
- Beschreibe die Schnittkurven der Ebene mit den beiden Zylindern!
- Drehe die Schnittkurve in Richtung der xy-Ebene, in Richtung der xz-Ebene und in Richtung der yz-Ebene und beschreibe die einzelnen Ansichten der Schnittkurve!
- Variiere die Radien der beiden Zylinder (geringfügig) und beschreibe die Form der Schnittkurven!
Zurück zu Schnitte von räumlichen Objekten | Lernpfad: GeoGebra - Grafik 3D