Der Tetraeder

tm.jpg

Der Tetraeder („Vierflächer“) ist eine dreiseitige Pyramide. Sind die Seitenfläche vier gleichseitige Dreiecke, so liegt ein regelmäßiger Tetraeder (einer der platonischen Körper vor.

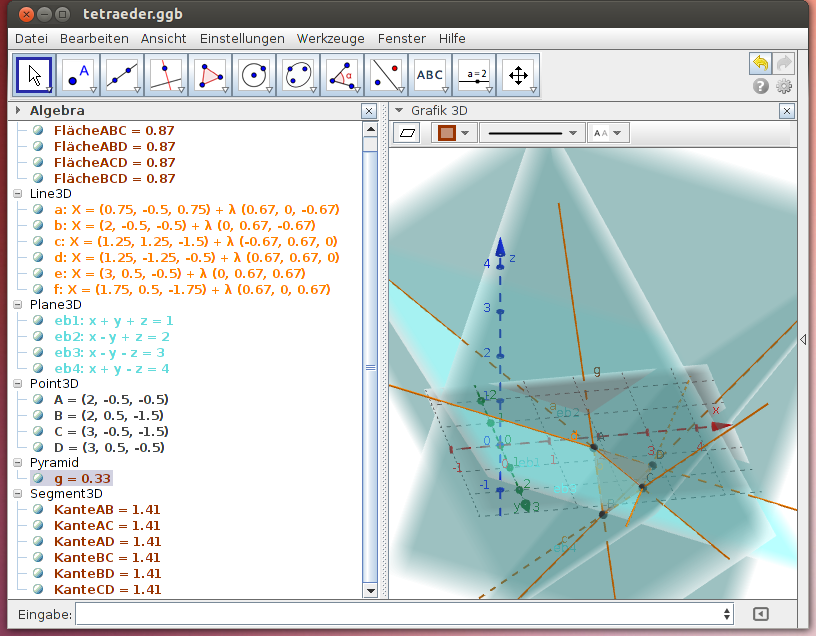
Im folgenden GeoGebra-Beispiel bilden die vier Ebenen 

eb1: x + y + z = 1
eb2: x - y + z = 2
eb3: x - y - z = 3
eb4: x + y - z = 4

mit ihren Schnittgeraden die Seitenkanten eines Tetraeders:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Hinweis: Ein regelmäßiger Tetraeder kann mit dem GeoGebra-Werkzeug erzeugt werden.

Aufgaben:

  • Begründe, dass im obigen GeoGebra-Beispiel ein regelmäßiger Tetraeder vorliegt!
  • Beschreibe die Eigenschaften der Ecken, Kanten und Seitenflächen!
  • Jeder Tetraeder (nicht nur der regelmäßige) hat eine Umkugel - lies nach!
  • Jeder Tetraeder (nicht nur der gleichmäßige) hat eine Inkugel - lies nach!
  • Lies zum Tetraeder nach (WikiPedia:Tetraeder)!

Zurück zu Lernpfad: GeoGebra - GeoGebra 3D | Platonischer Körper


Zuletzt angesehen: • geomr_03 • amplitude • qu_fkt_hl • rollkurve • tetraeder