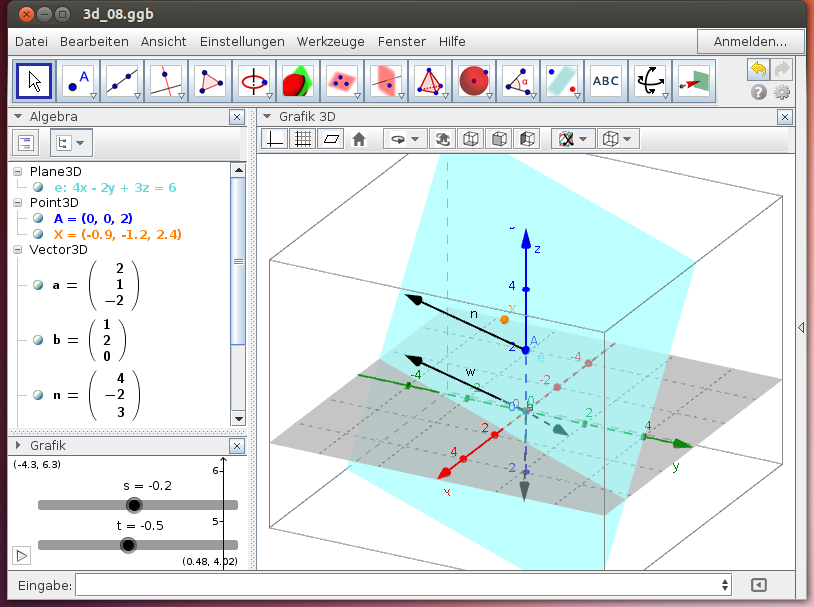
Ebenengleichung in Normalvektorform
Eine Ebene kann mit ihrem Normalvektor ![tex:\vec n]() und einem Einstiegspunkt A festgelegt werden. Dann gilt für jeden Punkt X in der Ebene:
und einem Einstiegspunkt A festgelegt werden. Dann gilt für jeden Punkt X in der Ebene:
Beispiel:
Stelle für den Punkt A(0|0|2) und den beiden Richtungsvektoren die Ebenengleichung in Normalvektorform auf!
Ergebnis: Die Ebenengleichung lautet 4x - 2y + 3z = 6 (Rechne nach!).
Aufgaben:
- Vergleiche mit der Ebenengleichung in Parameterdarstellung!
- Überprüfe im obigen Geogebra-Beispiel mit Hilfe der beiden Schieberegler s und t, dass der Punkt
stets auf der Ebene 4x - 2y + 3z = 6 liegt!
- Gib die Gleichungen der xy-Ebene, der xz-Ebene und der yz-Ebene des Koordinatensystems in Normalvektorform und als lineare Gleichungen in drei Variablen an!
Zurück zu Analytische Geometrie des Raumes