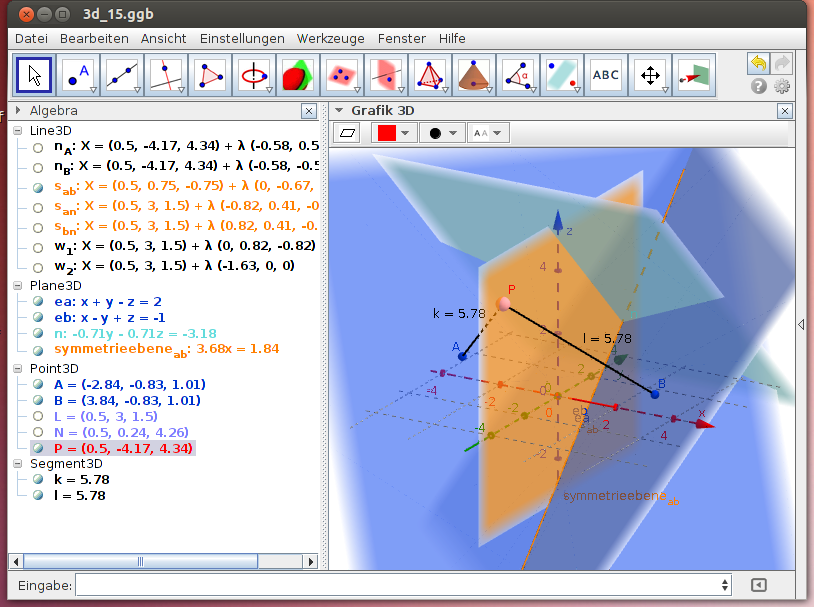
Symmetrieebene zweier Ebenen ("Winkelhalbierende")
Zwei einander schneidende Ebenen haben eine Symmetrieebene, deren Punkte von den beiden gegebenen Ebenen jeweils den gleichen (Normal-)Abstand haben. Überprüfe dies anhand des folgenden GeoGebra-Beispiels:
Aufgaben:
- Beschreibe die Konstruktion der Symmetrieebene!
- Verschiebe den Punkt P auf der Symmetrieebene und vergleiche die Abstände zu den beiden Ebenen!
Hinweis: Verschiebe den Punkt P auf der Symmetrieebene indem du den Punkt in der Grafik 3D-Ansicht fokussierst. Da der Punkt an die Ebene gebunden ist, lässt er sich nur auf dieser verschieben:
- Begründe, warum die Konstruktion der Symmetrieebenen für die Konstruktion der Inkugel eines Tetraeders von Bedeutung ist!
Zurück zu Lernpfad: GeoGebra - Grafik 3D | Inkugel