Der Winkel zwischen 2 Vektoren im Raum
Berechne den Winkel zwischen zwei Vektoren im Raum mit der vektoriellen Winkelformel (analog zu Vektoren in der Eben):
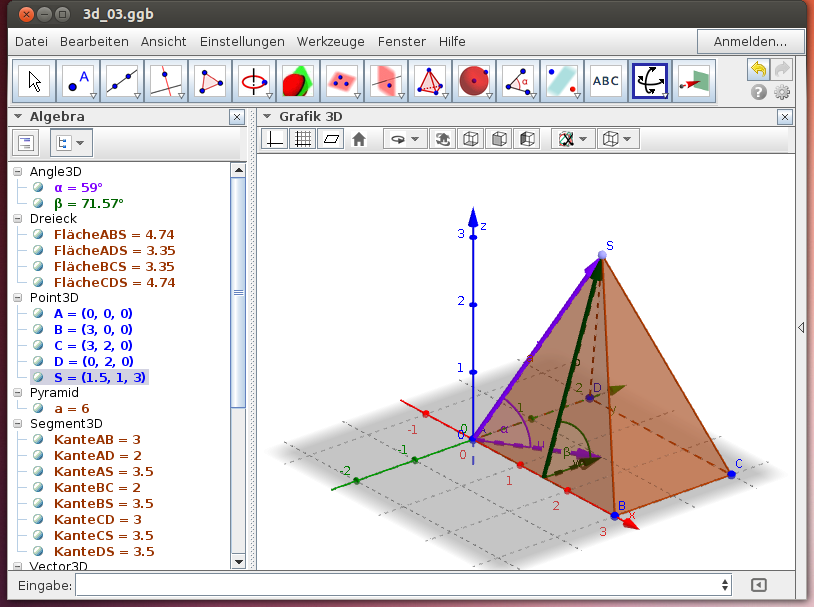
Eine Pyramide ist durch das Basisrechteck ABCD[A(0|0|0), B(3|0|0), C(3|2|0), D(0|2|0)] und durch die Spitze S(1.5|1|3) festgelegt. Bestimme die Winkel α zwischen dem Vektor von A nach S („Seitenkante“) und der Basis und den Winkel β zwischen der Seitenfläche ABS und der Basis und vergleiche die beiden Winkel!
Ergebnis: Der Winkel α ist (deutlich) kleiner als der Winkel β. Begründe dies!
Zurück zu Analytische Geometrie des Raumes