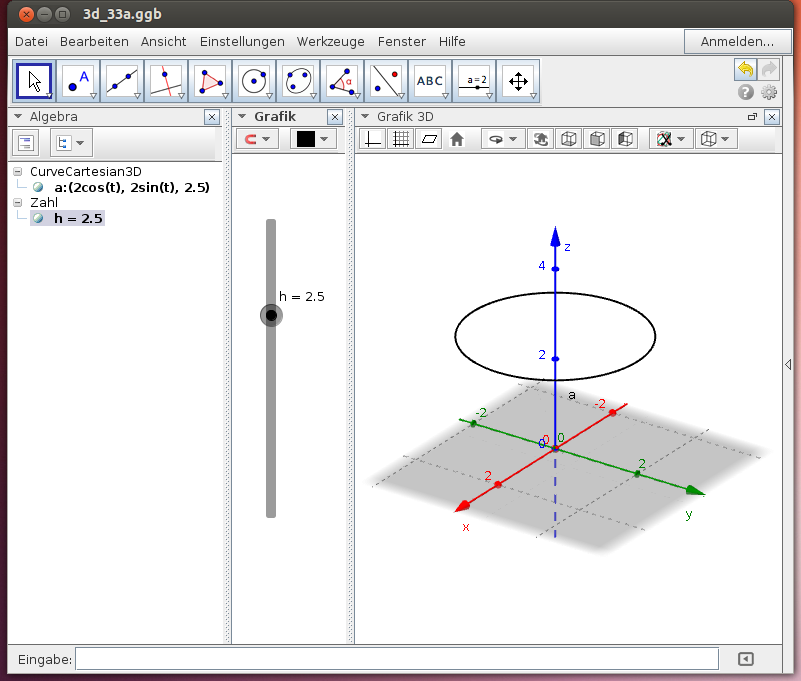
Horizontale Kreise
Die Parameterdarstellung X(t) = (x(t), y(t), z(t)), t ∈ [a;b] weist jedem Parameterwert t eindeutig einen Punkt P im Raum zu. Es entsteht dabei eine Raumkurve a.
Die Parameterdarstellung (2 cos(t), 2 sin(t), h) für t ∈ [0; 2π] legt einen horizontalen Kreis fest, der h Einheiten oberhalb der xy-Ebene verläuft.
Aufgaben:
- Variiere im obigen GeoGebra-Beispiel h mit dem Schieberegler und beobachte die Position des Kreises!
- Lege weitere Kreise, parallel zur xz-Ebene, oder parallel zur yz-Ebene fest!
Zurück zu Kurven und Flächen im Raum