Die Ebenengleichung in Parameterform

tm.jpg 6, S. 108 - 109

Jeder Punkt X der Ebene kann durch eine geeignete Kombination aus Einstiegspunkt A und zwei Richtungsvektoren tex:\vec u und tex:\vec v erreicht werden:

tex:X(s,t) = A + s \cdot \vec u + t \cdot \vec v

(s, t … Parameter)

Beispiel:

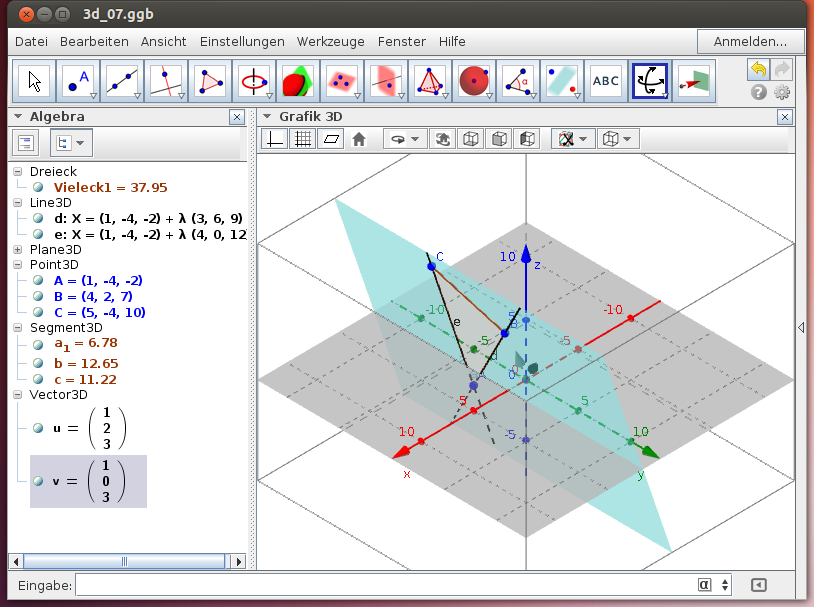
Stelle die Ebene dar, die durch die drei Punkte A(1|-4|-2), B(4|2|7) und C(5|-4|10) festgelegt wird! Gib eine Parameterdarstellung der Ebene an!

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Ergebnis: X(s,t) = (1,-4,2) + s (1,2,3) + t (1,0,3)

Aufgaben:

  • Vergewissere dich durch geeignetes Drehen der Darstellung, dass das Basisdreieck ABC tatsächlich in der Ebene liegt!
  • Begründe, dass die Darstellung einer Ebene in Parameterdarstellung nicht eindeutig ist!
  • Vergleiche mit der Ebenengleichung in Normalvektorform!

Zurück zu Analytische Geometrie des Raumes


Zuletzt angesehen: • 3d_01 • 3d_03 • 3d_04 • 3d_06 • 3d_07