−Inhaltsverzeichnis
Schnittgerade zweier Ebenen
Sind zwei Ebenen nicht parallel, so haben sie eine Gerade gemeinsam (Schnittgerade).
Beispiel: Berechne die Schnittgerade der beiden Ebenen e1: x - 3y + 2z = 3 und e2: 3x + y - z = 1!
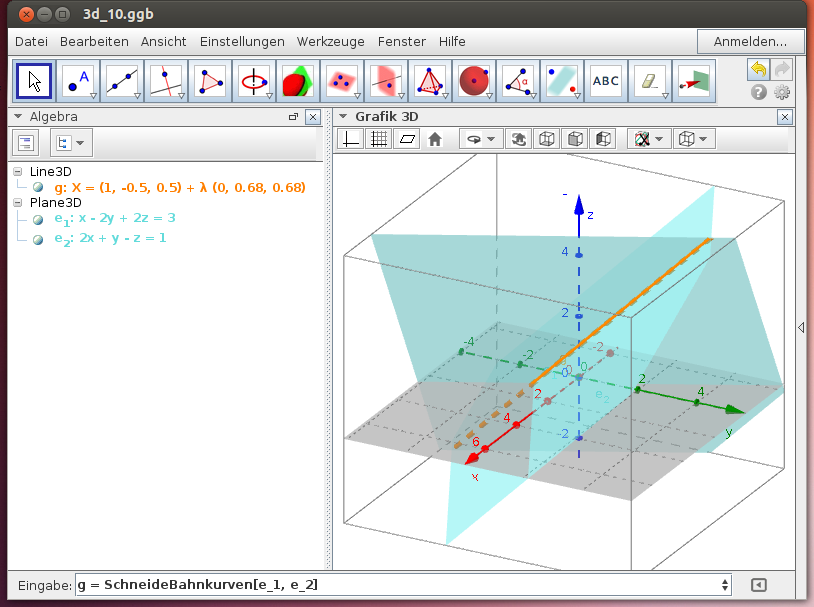
Lösung in der Grafikansicht Grafik 3D
Gib die beiden Ebenengleichungen in Normalvektorform als Gleichungen in den drei Variablen x, y und z ein und bestimme die Schnittgerade mit dem GeoGebra-Werkzeug Schneide(<Objekt1>,<Objekt2>):
Ergebnis: g: X(t) = (1|-0.5|-0.5) + t (0|0.68|0.68)
Lösung mit dem CAS
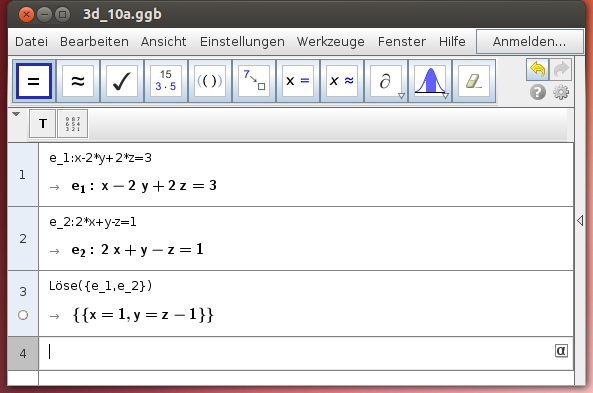
Gib die beiden Ebenengleichungen ein und Löse das Gleichungssystem der beiden linearen Gleichungen in den 3 Unbekannten x, y und z:
Ergebnis:
Wähle z als Parameter t!
x(t) = 1 y(t) = -1 + t z(t) = t
Zurück zu Analytische Geometrie des Raumes