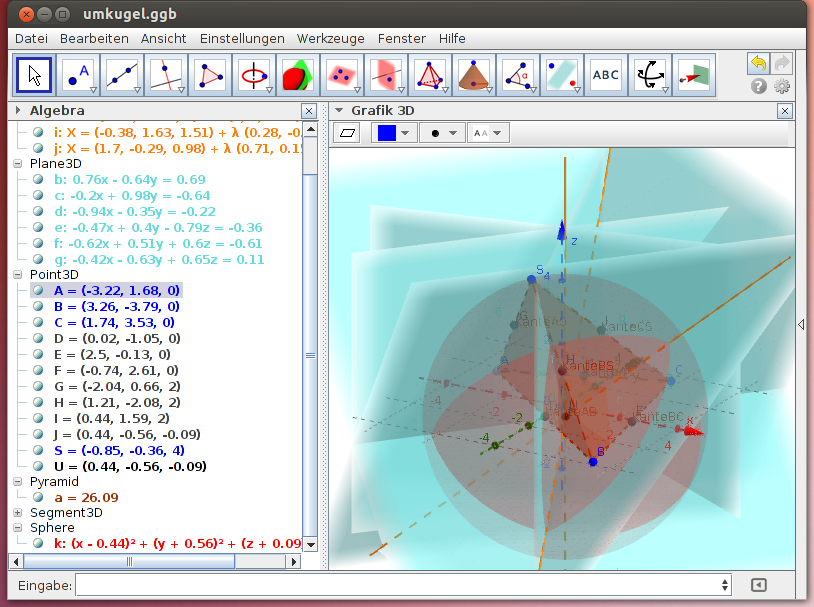
Umkugel eines Tetraeders
Eine Kugel wird durch Mittelpunkt und Radius, durch Mittelpunkt und einen weiteren Punkt der Kugeloberfläche oder - allgemein - durch 4 Punkte der Kugeloberfläche festgelegt. Daher hat jeder allgemeiner Tetraeder eine Umkugel. Beobachte diese im folgenden GeoGebra-Beispiel:
Aufgaben:
- Gib die Eigenschaften der Symmetrieebene einer Strecke an!
- Beschreibe den Konstruktionsgang der Umkugel: Der Mittelpunkt U der Kugel hat von jedem Eckpunkt des Tetraeders den gleichen Abstand. Insbesondere muss der Umkreismittelpunkt von je zwei Eckpunkten den gleichen Abstand haben …
- Recherchiere zu den Platonischen Körpern und überprüfe, dass diese alle eine Umkugel besitzen!
- Überprüfe, dass jedes quadratische Prisma und jede quadratische Pyramide eine Umkugel besitzen!
Zurück zu Lernpfad: GeoGebra - GeoGebra 3D | Inkugel