Die Viviani-Kurve
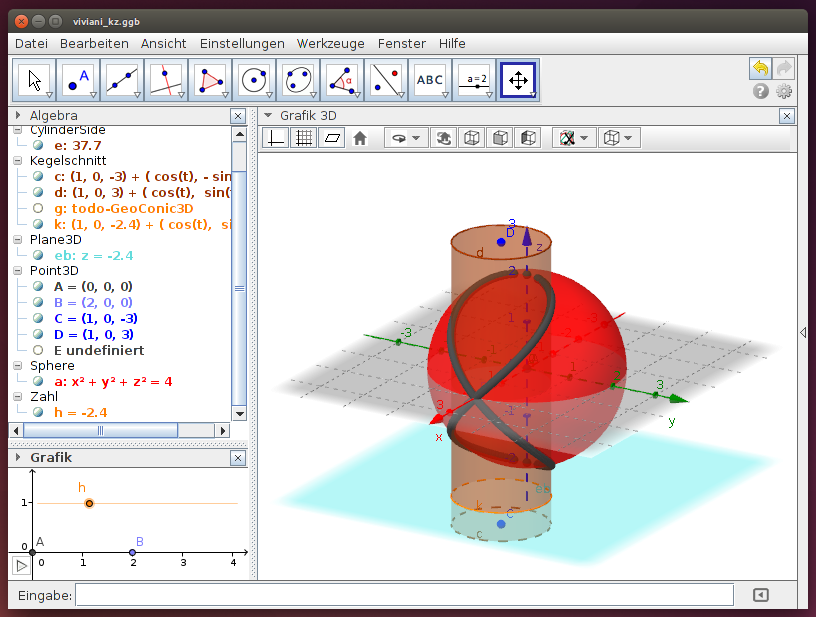
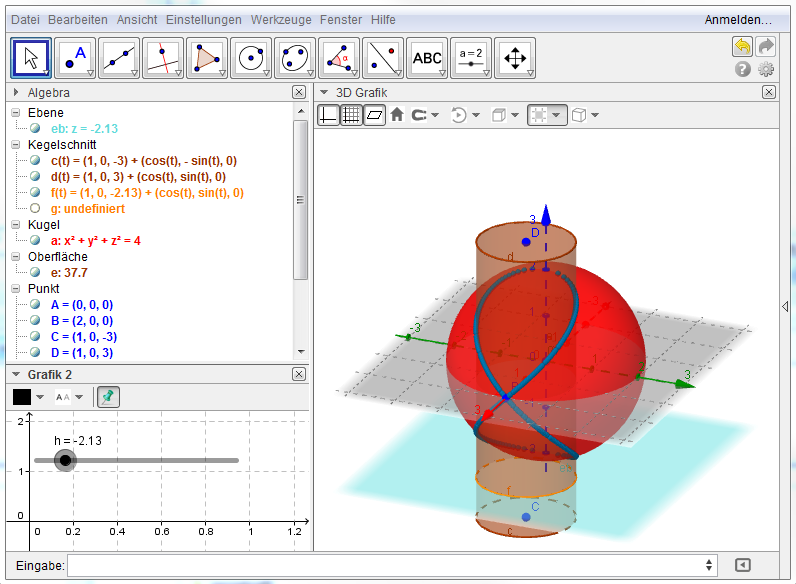
Wir betrachten eine Kugel und einen Kreiszylinder, dessen Durchmesser dem Kugelradius entspricht. Ist eine Erzeugende dieses Kreiszylinders eine Kugelachse, dann ergibt die Schnittkurve die Viviani-Kurve:
Hinweis: Sowohl die Kugel als auch der Zylinder werden durch die Horinzontalebene geschnitten. Die Schnittpunkte der beiden Schnittkreise ergeben jeweils zwei Punkte der Viviani-Kurve. Die Animation des Schiebereglers h bewirkt die Parallelverschiebung der Ebene, sodass alle Schnittkreise der Kugel und des Drehzylinders bestimmt werden …
Aufgaben:
- Öffne die obige GeoGebra-Datei und erzeuge die Viviani-Kurve als Punktespur durch Animation des Schiebereglers für h!
- Drehe die Abbildung in Richtung der xy-Ebene, in Richtung der xz-Achse und in Richtung der yz-Achse und vergleiche die Punktespur mit den Schattenprojektionen der Viviani-Kurve!
Hinweis: Die Betaversion von GeoGebra 3D wird zur Zeit häufig aktualisiert
3D-Grafikfenster (August 2014)
Zurück zu Schnitte von räumlichen Objekten | Lernpfad: GeoGebra - Grafik 3D