Inhaltsverzeichnis
Reelle Funktionen
Die Eigenschaften von Funktionen liest du am besten von ihren Funktionsgraphen ab. GeoGebra unterstützt dich dabei - durch die Darstellung der Funktionsgraphen in der Grafik-Ansicht und mit dem Werkzeug Funktionsinspektor!
Nullstellen und Fixpunkte
Monotonie und Extremstellen
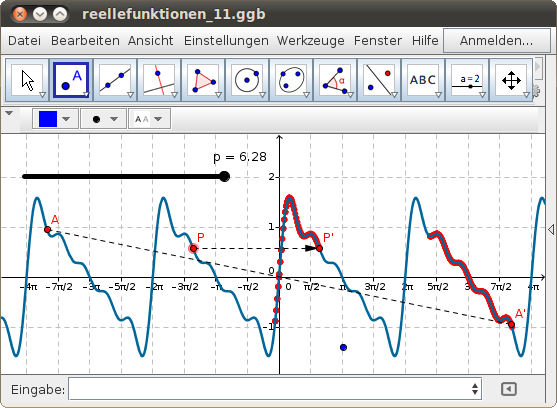
Symmetrie und Periodizität
Bijektive Funktion und Umkehrfunktion
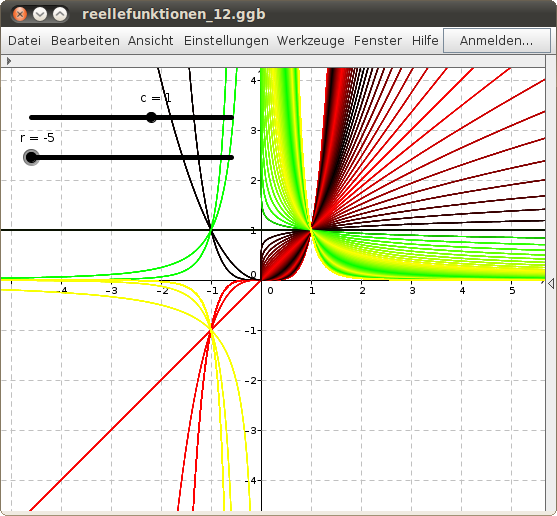
Potenzfunktion
Polynomfunktion und gebrochen rationale Funktion
- Polynomfunktionen - Von einer Polynomfunktion 3. Grades sind vier Funktionswerte bekannt. Bestimme den Funktionsterm!
Exponentialfunktion
Untersuche die Eigenschaften der Exponentialfunktionen mit Hilfe der Parametervariation:
- f(x) = a b^x (zu BIFIE: FA5.3)
- f(x) = a exp(b x) (zu BIFIE: FA5.3)
Untersuche bemerkenswerte Eigenschaften der Exponentialfunktion :
- f(x + 1) = b f(x) (zu BIFIE: FA5.4)
- Verdopplungszeit / Halbwertszeit (zu BIFIE: FA5.5)
Die Exponentialfunktion und die Exponentialfunktion
hängen eng zusammen. Untersuche dies an Hand des Funktionsgraphen und an Hand der Tabellenwerte in folgendem Beispiel:
- Exponentialfunktionen in Anwendungen (zu BIFIE: FA 5.1)
Exponentialfunktionen beschreiben Wachstums- und Zerfallsprozesse in einfachen Modellen. Folgende Beispiele fassen grundsätzliche Eigenschaften zusammen:
Logarithmusfunktion
Sinus, Cosinus und Tangens für beliebige Winkel
Winkelfunktionen
Untersuche die Eigenschaften der Sinusfunktion mit Hilfe der Parametervariation:
- f(x) = a sin(b x) (zu BIFIE: FA6.3)
Die folgenden Beispiele aus der Physik / Technik beschreiben die Eigenschaften von harmonischen Schwingungen. Jede harmonische Schwingung wird durch eine Sinus- oder Cosinuskurve beschrieben.
- Periode und Frequenz einer Sinus- oder Cosinuskurve
- Zusammengesetzte Schwingungen
Anmerkung: Für harmonische Wellen stellen wir oft ihre augenblickliche Schwingungsform abhängig vom Ort (zB. der Entfernung vom Ausgangspunkt der Welle) dar. Diese ist eine Funktion des Ortes, z.B. f(x) = 0,0065 sin (1.2 x).