Exponentielle Zusammenhänge in Tabellen und als Exponentialfunktion erkennen

(zu tm.jpg 6)

BIFIE Grundkompetenz FA5.1 (Inhaltsbereich Funktionale Abhängigkeiten, Exponentialfunktion tex:f(x) = a \cdot b^x bzw. tex:f(x) = a \cdot e^{\lambda \cdot x} mit tex:a, b \in \mathbf{R}^+, \lambda \in \mathbf{R})

Verbal, tabellarisch, grafisch oder durch eine Gleichung (Formel) gegebene exponentielle Zusammenhänge als Exponentialfunktion erkennen bzw. betrachten können; zwischen diesen Darstellungsformen wechseln können.

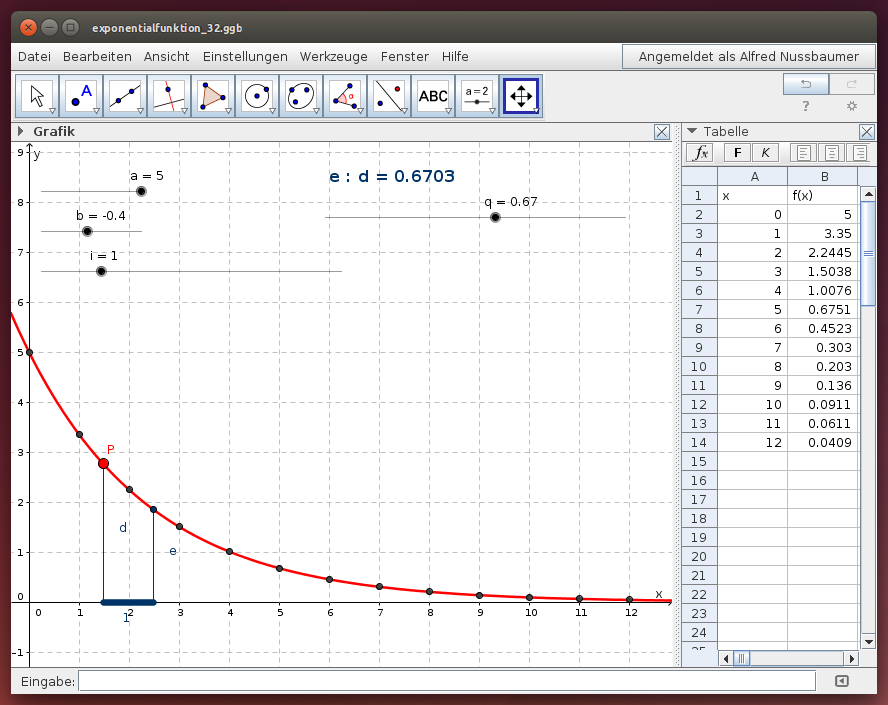
Wähle die Parameter a und b (und somit einen Anfangswert) im folgenden GeoGebra-Beispiel und berechne den folgenden Funktionswert durch Multiplikation mit dem Faktor q. Setze iterativ fort und ermittle so die Werte nach 1, 2, 3, … 12 Zeitschritten. Vergleiche diese Werte mit den Funktionsgraphen der Exponentialfunktion tex:f(x) = a e^{b x} und wähle einen solchen Wert für q, sodass die Tabellenwerte genau auf dem Funktionsgraphen zu liegen kommen:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Vergleiche die Werte der Parameter a, b und q und gib an, ob Gleichheit besteht!
  • Vergleiche den Quotienten e/d mit q: Gib den Zusammenhang an und begründe diesen!
  • Nenne Anwendungsbeispiele für die iterative Berechnung von Tabellenwerten (wie im obigen GeoGebra-Beispiel für Wachstums- und Zerfallsprozesse (Hinweis: Jährlicher Zuwachs an Gütern, Kapital, … stündlicher Zerfallsprozesse …)!

zurück zu Reelle Funktionen | Eigenschaften der Exponentialfunktionen


Zuletzt angesehen: • geogebra-eingabezeile • einstieg • exponentialfunktion_30 • exponentialfunktion_31 • exponentialfunktion_32