Harmonische Schwingungen
Harmonische Schwingungen sind ein wichtiges Anwendungsbeispiel für Winkelfunktionen: Jede harmonische Schwingung lässt sich mit Hilfe von Cosinus- oder Sinusfunktionen darstellen.
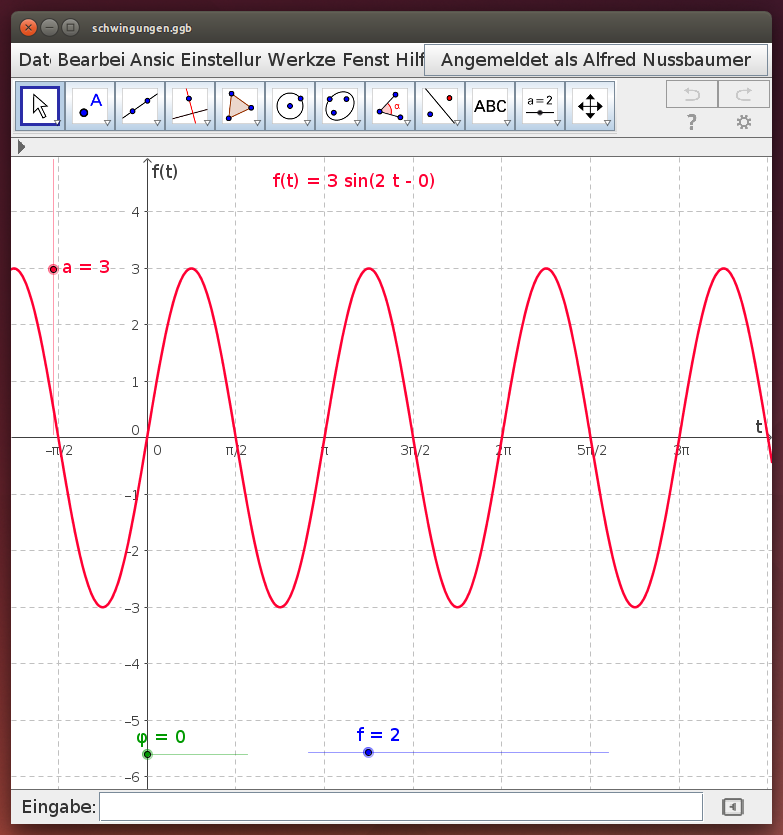
Das Zeit-Weg-Diagramm einer harmonischen Schwingung ist eine Sinus- oder Cosinuskurve. Die maximale Entfernung von der x-Achse ist die Amplitude, die Anzahl der Perioden in einer Zeiteinheit (Δt = 6.28) die Frequenz, und die Entfernung des „Startpunkts“ der Sinusfunktion vom Koordinatenursprung die Phasenverschiebung.
Untersuche im folgenden GeoGebra-Applet, wie die Form der Sinuskurve von der Amplitde a, von der Frequenz f und vom Phasenwinkel abhängt:
Aufgaben:
- Wähle mit den Schiebereglern verschiedene Werte für Amplitude, Frequenz und Phasenverschiebung. Beschreibe die Form der Sinuskurve und dokumentiere ihre Formel!
- Lies die Anzahl der Perioden für das Zeitintervall Δt = 6.28 s aus der Zeichnung ab und vergleiche mit der Schwingungsfrequenz f!
Weiter zu Harmonische Wellen | reelle Funktionen | Parametrisierte Kurven