Logarithmusfunktion
Die Logarithmusfunktion f(x) = alog x ist die Umkehrfunktion zur Exponentialfunktion f(x) = ax (a ≠ 1).
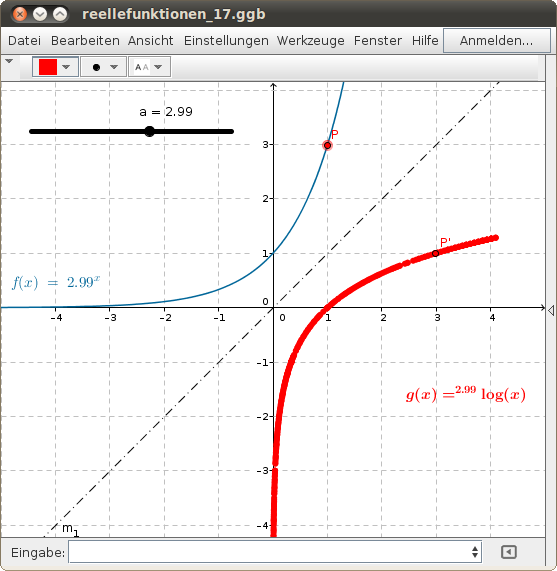
Stelle die Umkehrfunktion zur Exponentialfunktion mit dem folgenden GeoGebra-Beispiel dar:
Aufgaben:
- Begründe, warum für die Basis a = 1 der Exponentialfunktion f(x) = ax keine Umkehrfunktion existiert!
- Lies Eigenschaften der Logarithmusfunktion aus den Eigenschaften der Exponentialfunktion ab!
- Wähle verschieden große Werte für a und beschreibe die Auswirkung auf die Logarithmusfunktion!
Zurück zu reelle Funktionen | Funktionsinspektor