Umkehrfunktionen
Jede bijektive Funktion f hat eine Umkehrfunktion f-1:
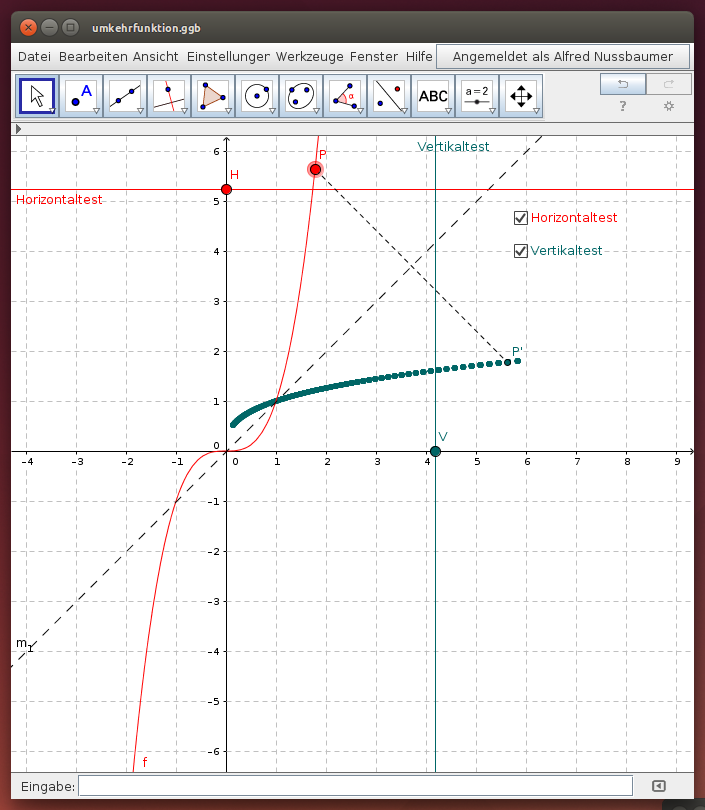
Der Graph der Umkehrfunktion f-1 ist symmetrisch zum Graph der Funktion f; die Symmetrieachse ist die 1. Mediane.
Verschiebe im folgenden GeoGebra-Beispiel den roten Punkt P auf dem Funktionsgraphen von f und beobachte die Spur des Punktes P'! Ist der Graph der Funktion f-1 symmetrisch zum Funktionsgraph von f bezüglich der 1. Mediane m1?
Aufgaben:
- Untersuche, ob die gegebene Funktion bijektiv ist: Schneidet die horizontale Gerade c den Funktionsgraphen von f genau einmal (im Punkt P) (Horizontaltest)?
- Untersuche, ob die Umkehrfunktion tatsächlich eine Funktion ist: Schneidet die vertikale Gerade c' den Funktionsgraphen von f-1 genau einmal (im Punkt P') (Vertikaltest)?
- Gib weitere Funktionen in der Eingabezeile ein, zB f(x) = x^2, f(x) = sin(x), f(x) = x^3, … und untersuche, ob die Funktion eine Umkehrfunktion besitzt (Hinweis: Mit <STRG> F kannst Du eine bestehende Spur löschen)!
- Verschiebe die gegebene Funktion und ermittle den Graph der Umkehrfunktion. Vergleiche den Graph der Funktion mit dem Graph der Umkehrfunktion! Wo liegen die Schnittpunkte der beiden Graphen?
Zurück zu Reelle Funktionen