Die Abhängigkeit des Funktionsgraphen der Polynomfunktion vom Grad n
6, S. 144 - 145, BIFIE GK FA4.1
(BIFIE: Der Zusammenhang zwischen dem Grad der Polynomfunktion und der Anzahl der Null-, Extrem- und Wendestellen sollte für beliebige n bekannt sein, konkrete Aufgabenstellungen beschränken sich auf Polynomfunktionen bis zum Grad n = 4.)
BIFIE Grundkompetenz FA4.1 (Inhaltsbereich Funktionale Abhängigkeiten, Polynomfunktion ![tex:f(x) = \sum_{i=0}^n a_i \cdot x^i]()
mit ![tex:n \in \mathbf{N}]()
)
Typische Verläufe von Graphen in Abhängigkeit vom Grad der Polynomfunktion (er)kennen.
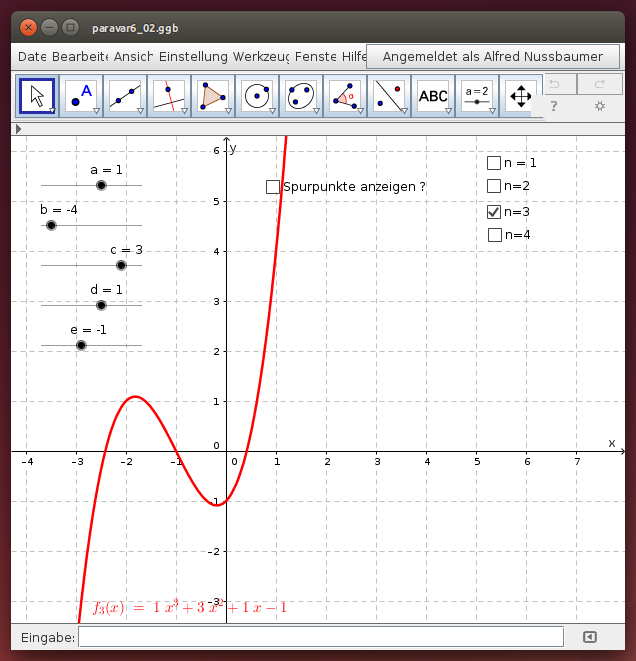
Wähle im folgenden GeoGebra-Applet den Grad n der Polynomfunktion mit Hilfe der Kontrollkästchen und beschreibe den Verlauf des Graphen:
Aufgaben:
- Vergleiche die Graphen der Polynomfunktionen für verschiedenen Grad n und beschreibe, wie die Eigenschaften des Funktionsgraphen vom Grad n abhängen!
- Ermittle für jeden Grad n (mit verschiedenen Parametern) die maximale Anzahl von Spurpunkten und beschreibe, wie diese Anzahl mit dem Grad n zusammenhängt (Hinweis: Gib an, wie viele Schnittpunkte der Graph mit der y-Achse und wie viele Schnittpunkte der Graph mit der x-Achse jeweils hat)!
zurück zu Reelle Funktionen
