Unerade Funktionen

tm.jpg 6, S. 138

  • Eine umgerade Funktion liegt vor, wenn für alle x aus Df f(-x) = - f(x) gilt.

Der Graph einer ungeraden Funktion ist punktsymmetrisch zum Koordinatenursprung.

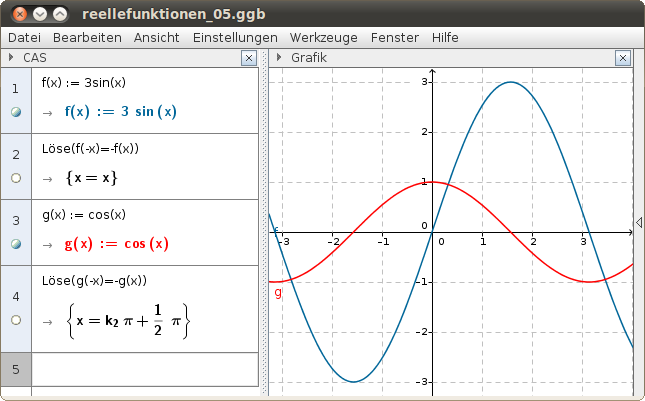
Begründe, warum die Funktion tex:f(x) = 3 \sin (x) im folgenden GeoGebra-Beispiel eine ungerade Funktion ist, und warum die Funktion tex:g(x) = \cos x keine ungerade Funktion ist:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Wähle weitere Funktionen und überprüfe, ob sie ungerade Funktionen sind!
  • Formuliere analoge Gleichungen für gerade Funktionen und überprüfe diese Eigenschaft an verschiedenen Beispielen!

Zurück zu Reelle Funktionen


Zuletzt angesehen: • reellefunktionen_05