Inhaltsverzeichnis
Lernpfad GeoGebra - Funktionsinspektor
5, S. 101 - 145, Themenheft Mathematik mit GeoGebra 5-6, Themenheft Mathematik mit GeoGebra 7-8
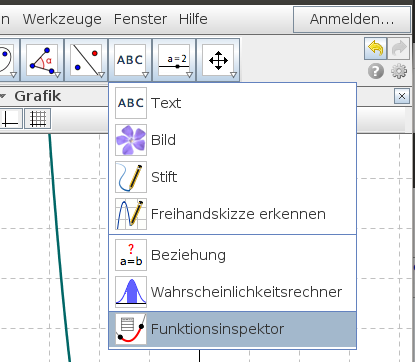
Der Funktionsinspektor dient zum Untersuchen der Eigenschaften von Funktionen. Er wird über das Funktionsinspektor-Icon 
aufgerufen:
Wähle anschließend die Funktion aus, die untersucht werden soll!
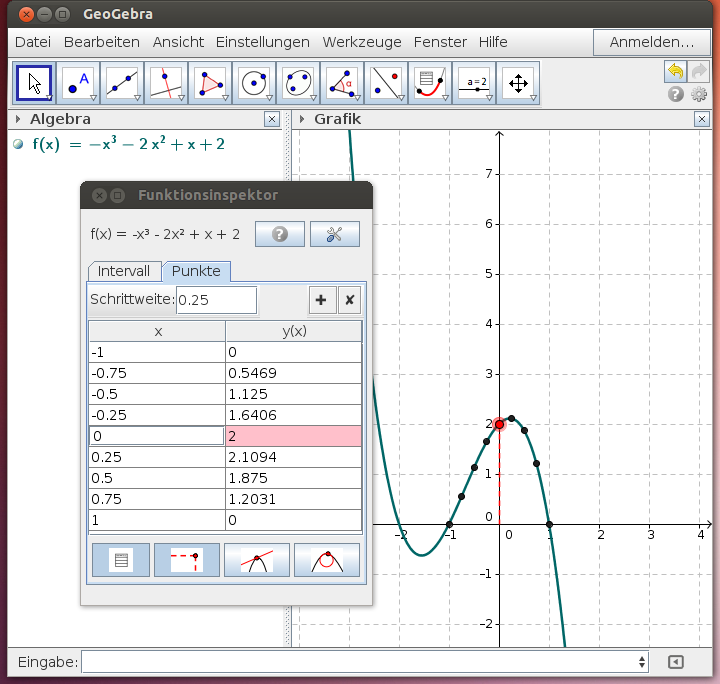
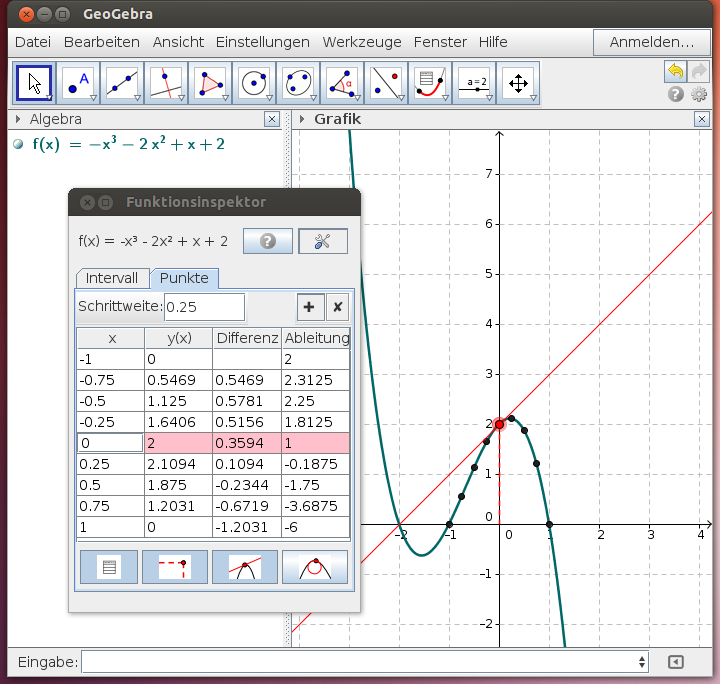
Funktionswertetabelle
Eine elementare Aufgabe besteht darin, Funktionswerte in einem bestimmten Bereich zu bestimmen. Wähle dazu im Funktionsinspektor den Karteireiter Punkte aus und wähle eine passende Schrittweite. Verschiebe den rot dargestellten Punkt auf dem Funktionsgraphen, um den gewünschten Bereich zu wählen!
Aufgaben:
- Wähle eine gebrochen rationale Funktion und untersuche ihre Eigenschaften mit Hilfe des Funktionsinspektors!
- Wähle eine Exponentialfunktion und untersuche ihre Eigenschaften mit Hilfe des Funktionsinspektors!
- Wähle eine trigonometrische Funktion und untersuche ihre Eigenschaften mit Hilfe des Funktionsinspektors!
- Wähle eine Logarithmusfunktion und untersuche ihre Eigenschaften mit Hilfe des Funktionsinspektors!
Änderungsraten, Tangenten, Ableitungen, Krümmung
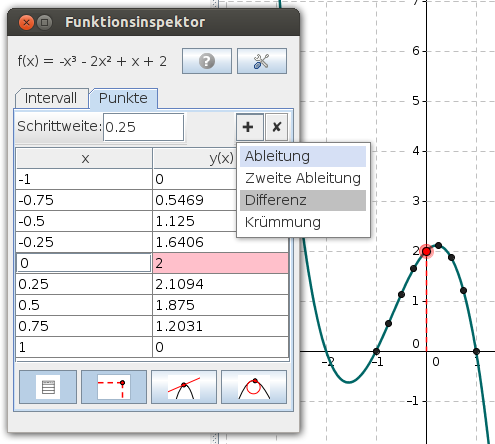
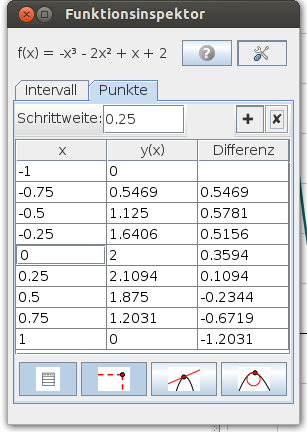
Die - auf die gewählte Schrittweite bezogenen Änderungsraten lassen sich mit 
zu den schon angezeigten Spalten hinzufügen.
Zur Auswahl stehen folgende Spalten:
Die jeweils letzte Spalte kann mit 
gelöscht werden.
Weiters können im gewählten Punkt die Tangente und der Krümmungskreis angezeigt werden:
Aufgaben:
- Untersuche, wie die Tangente und die Ableitung zusammenhängen!
- Untersuche und beschreibe Zusammenhänge zwischen dem Krümmungskreis und der 2. Ableitung!
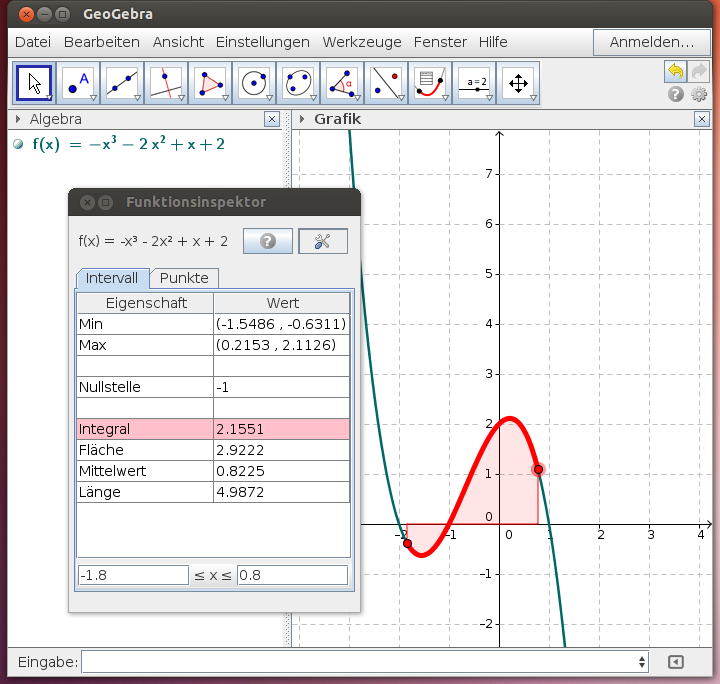
Eigenschaften der Funktion über einem gewählten Bereich
Mininum, Maximum, Nullstelle, Integral, Flächeninhalt, Mittelwert und Bogenlänge über einem Intervall können über den Karteireiter Intervall betrachtet werden:
Die Intervallgrenzen werden entweder in den Eingabefeldern oder durch Verschieben der roten Punkte auf dem Funktionsgraphen festgelegt.
Hinweis: Liegen mehrere Nullstellen im gewählten Intervall, so wird kein Wert ausgegeben.
Aufgaben:
- Erkläre, in welchen Fällen die Werte für Integral und Flächeninhalt voneinander abweichen!
- Untersuche, wie der Mittelwert vom gewählten Bereich abhängt!
Zurück zu Lernpfade | Funktionen | Reelle Funktionen
