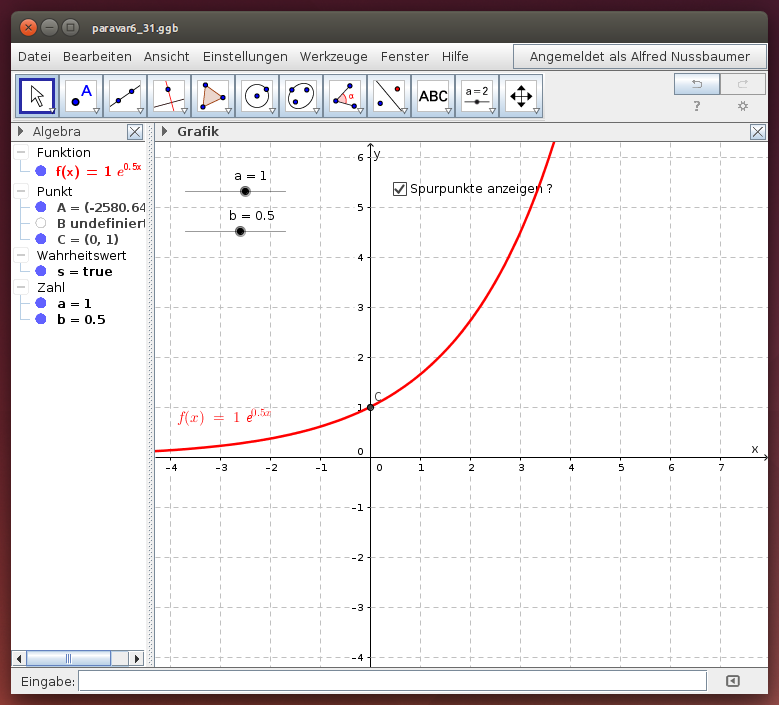
Die Exponentialfunktion f(x) = a e^(b x)
 6, BIFIE GK FA5.3
6, BIFIE GK FA5.3
BIFIE Grundkompetenz FA5.3 (Inhaltsbereich Funktionale Abhängigkeiten, Exponentialfunktion ![tex:f(x) = a \cdot b^x]() bzw.
bzw. ![tex:f(x) = a \cdot e^{\lambda \cdot x}]() mit
mit ![tex:a, b \in \mathbf{R}^+, \lambda \in \mathbf{R}]() )
)
Die Wirkung der Parameter a und b (bzw. ) kennen und die Parameter in unterschiedlichen Kontexten deuten können
Aufgaben:
- Variiere den Parameter a und beschreibe, wie die Form der Exponentialkurve vom Wert für a abhängt!
- Variiere den Parameter b und beschreibe, wie die Form der Exponentialkurve vom Wert für b abhängt!
- Betrachte die Spurpunkte der Funktion und gib die zugehörige Bedeutung an!
- Beschreibe, wo der „Anfangswert“ der Funktion liegt und gib den Zusammenhang mit obigen Parametern an!
zurück zu Reelle Funktionen | Eigenschaften der Exponentialfunktionen