Harmonische Wellen
Harmonische Wellen entstehen, wenn viele Objekte in gleicher Weise harmonisch schwingen können, und wenn die Schwingung von einem Objekt auf das benachbarte übertragen werden kann. Schwingen alle Objekte harmonisch, so entsteht eine harmonische Welle.
- Eine harmonische Welle liegt vor, wenn jedes Objekt der Welle harmonisch schwingt.
- Die Frequenz und die Amplitude jedes schwingenden Objekts ist zugleich Frequenz und Amplitude der Welle.
Im Idealfall sind alle Objekte gleich weit voneinander entfernt, und die Phasenverschiebung zwischen benachbarten Objekten ist überall die gleiche. Für die folgenden Darstellungen gehen wir davon aus, dass die Objekte senkrecht zur Ausbreitungsrichtung der Welle schwingen (eine Transversalwelle liegt vor). Dann ist die Wellenform eine Sinus- oder Cosinuskurve, deren Funktionswert von der Entfernung vom Ausgangspunkt der Welle abhängt.
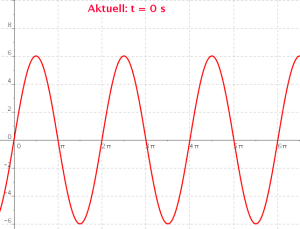
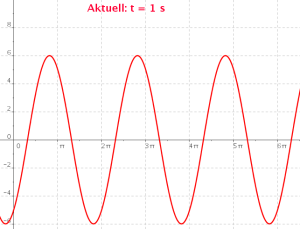
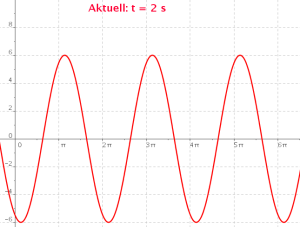
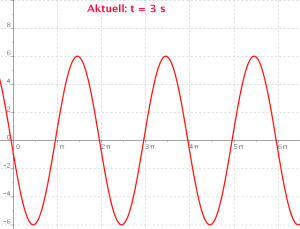
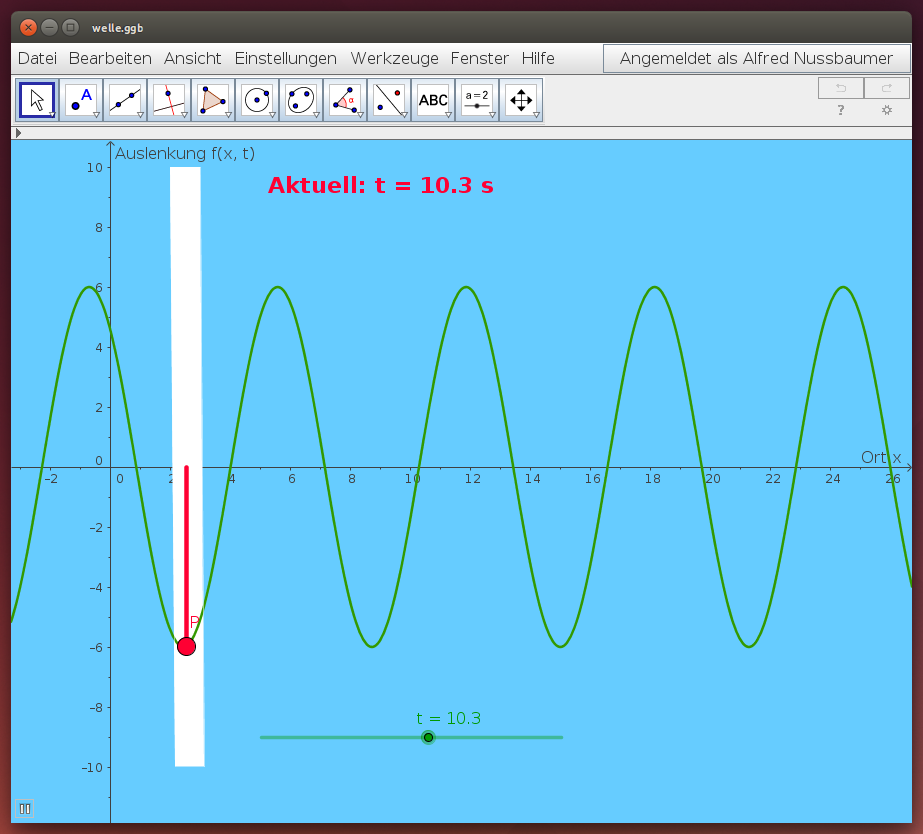
Betrachte im folgenden GeoGebra-Applet, wie ein einzelner Punkt der Welle schwingt. Die Abhängigkeit von der Zeit t wird dabei als Animation dargestellt:
Aufgaben:
- In der Physik werden die Maxima der Welle als Wellenberge, die Minima als Wellentäler bezeichnet. Beschreibe die Lage dieser Wellenberge und Wellentäler! Erläutere, wie die Welle weiter wandert!
- Wellen werden durch Funktionsterme beschrieben, die von zwei Variablen abhängen, vom Ort x und von der Zeit t: f(x,t) = … Dabei beschreibt f(x,t) die Auslenkung aus der Ruhelage an einem bestimmten Ort x zu einer bestimmten Zeit t. Überlege, welche Variablen für eine Wellenfunktion erforderlich sind, die die Wellen in einer Wanne beschreiben!
- Physikalisch bedeutet eine Welle stets einen Energietransport. Recherchiere Beispiele dazu und fasse zusammen!
Weiter zu Harmonische Schwingungen | reelle Funktionen | Parametrisierte Kurven | Winkelfunktionen