Inhaltsverzeichnis
Der Sinus im rechtwinkligen Dreieck - und im Einheitskreis
Um die Sinuswerte von beliebigen Winkel berechnen zu können haben wir in der Trigonometrie bereits die Definition der Winkelfunktionen am Einheitskreis kennen gelernt. Untersuche nun, warum die Definition am Einheitskreis wesentlich mächtiger ist als die Definition des Sinus im rechtwinkligen Dreieck:
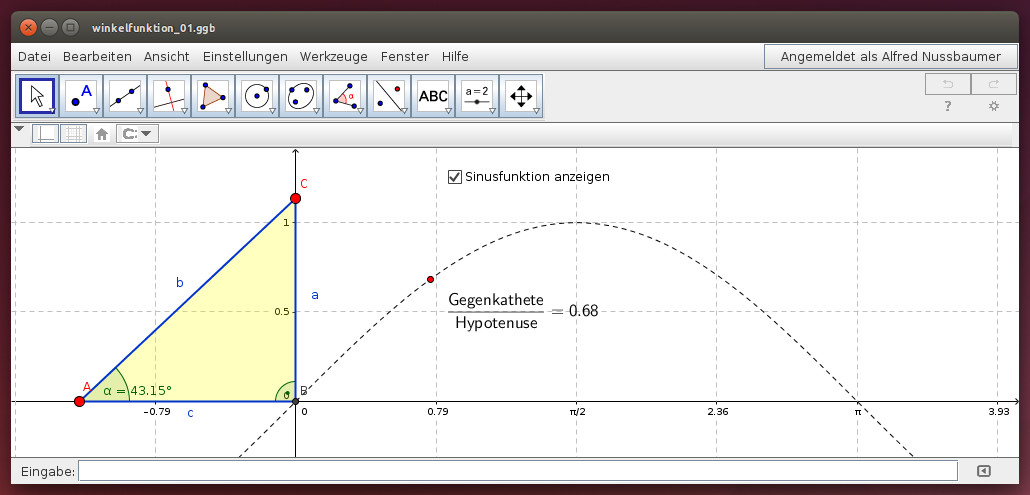
Das rechtwinklige Dreieck:
Verschiebe die Eckpunkte A und C des rechtwinkligen Dreiecks auf den Koordinatenachsen so, dass der Winkel α beliebige Werte zwischen 0° und 90° annimmt. Beobachte die Spur des Punktes P!
Aufgaben:
- Gib an, in welchem Intervall die Sinusfunktion an Hand des rechtwinkligen Dreiecks dargestellt werden kann!
- Begründe: Warum liegen die Werte der Sinusfunktion zwischen 0 und 1?
- Erstelle ein analoges GeoGebra-Applet für den Cosinus!
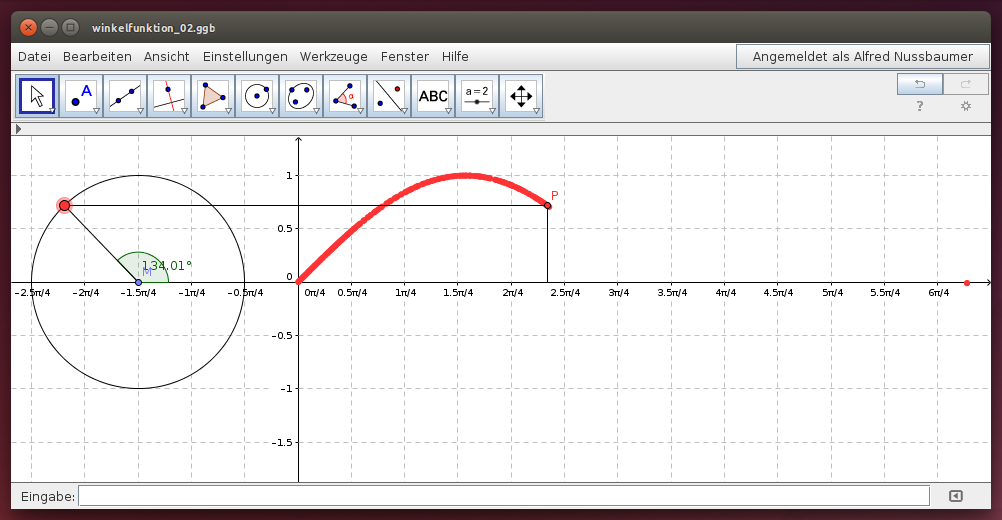
Der Einheitskreis:
Verschiebe den Punkt A auf der Kreislinie so, dass der Winkel α beliebige Werte zwischen 0° und 360° annimmt. Beobachte die Spur des Punktes P!
Aufgaben:
- Gib an, in welchem Bereich die Werte der Sinusfunktion liegen!
Zurück zu Trigonometrie (5. Klasse) | Reelle Funktionen (6. Klasse) | Winkelfunktionen