Bestimme und überprüfe die Periode von Funktionen!
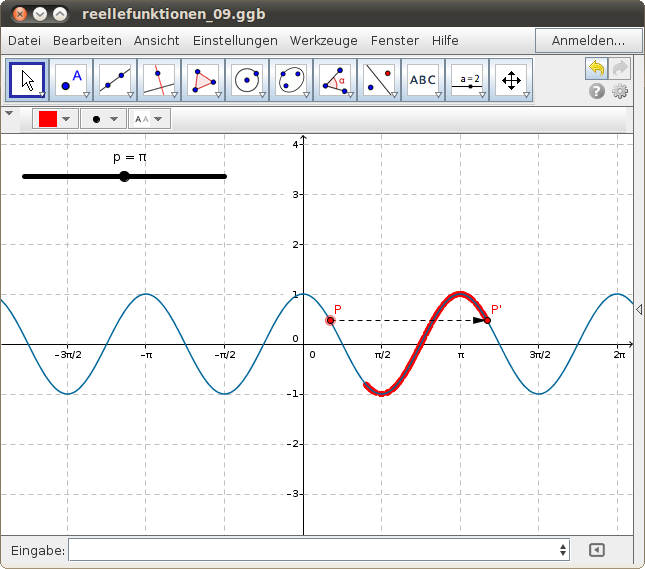
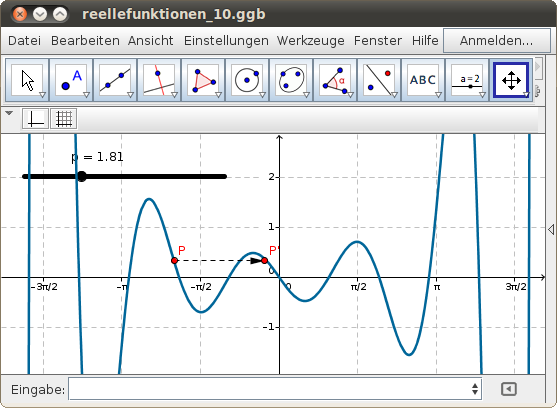
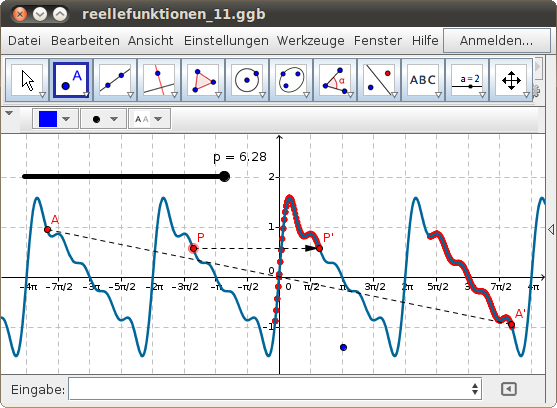
Für periodische Funktionen gilt f(x) = f(x+p), wobei p die Periode ist. Finde mit dem folgenden GeoGebra-Beispiel die Periode p und überprüfe, dass tatsächlich eine periodische Funktion vorliegt: Verschiebe den roten Punkt P auf dem Funktionsgraphen und beobachte die Spur von P'!
Aufgaben:
- Bestimme die Periode der Winkelfunktionen
,
und
!
- Wähle Kombinationen verschiedener Winkelfunktionen und überprüfe ihre Periodizität!
- Zeige, dass die folgende Funktion nicht periodisch ist:
- Untersuche den Funktionsgraphen
in Hinblick auf Symmetrie und Periodizität!
Zurück zu Reelle Funktionen