Eine charakteristische Eigenschaft der Exponentialfunktion ...
BIFIE Grundkompetenz FA5.5 (Inhaltsbereich Funktionale Abhängigkeiten, Exponentialfunktion ![tex:f(x) = a \cdot b^x]() bzw.
bzw. ![tex:f(x) = a \cdot e^{\lambda \cdot x}]() mit
mit ![tex:a, b \in \mathbf{R}^+, \lambda \in \mathbf{R}]() )
)
Die Begriffe Halbwertszeit und Verdoppelungszeit kennen, die entsprechenden Werte berechnen und im Kontext deuten können.
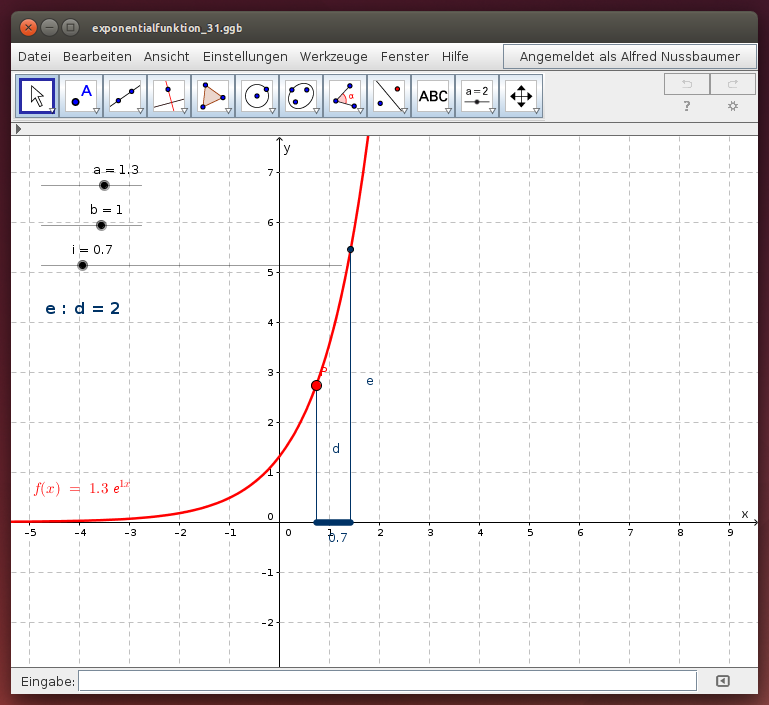
Im folgenden GeoGebra-Beispiel werden die Funktionswerte d = f(x1) und e = f(x2) ermittelt. Anschließend wird der Quotient e/d bestimmt und ausgegeben. Finde den Wert für i, sodass e = 2 d gilt:
Aufgaben:
- Wähle Parameter a und b und lies den Quotienten e/d ab!
- Wähle den Parameter i so, dass e = 2 d gilt!
- Verschiebe den roten Punkt P auf dem Funktionsgraphen und beobachte dabei den Quotienten e/d. Beschreibe das Ergebnis!
- Bei Wachstumsprozessen spricht man in obigem Zusammenhang von der Verdoppelungszeit. Lies dazu nach!
- Finde entsprechende Paraemter a und b so, dass ein Zerfallsprozess vorliegt und lies den Quotienten e/d ab!
- Wähle den Parameter i so, dass e = 0.5 d gilt!
- Verschiebe den roten Punkt P auf dem Funktionsgraphen und beobachte dabei den Quotienten e/d. Beschreibe das Ergebnis!
- Bei Zerfallsprozessen spricht man in obigem Zusammenhang von der Halbwertszeit. Lies dazu nach!
zurück zu Reelle Funktionen | Eigenschaften der Exponentialfunktionen