Inhaltsverzeichnis
Gebrochen rationale Funktionen
Gebrochen rationale Funktionen sind der Quotient zweier Polynomfunktionen. In den folgenden GeoGebra - Beispielen werden wir jeweils ein Zählerpolynom und ein Nennerpolynom festlegen und aus ihren Eigenschaften die Eigenschaften der Funktion
begründen.
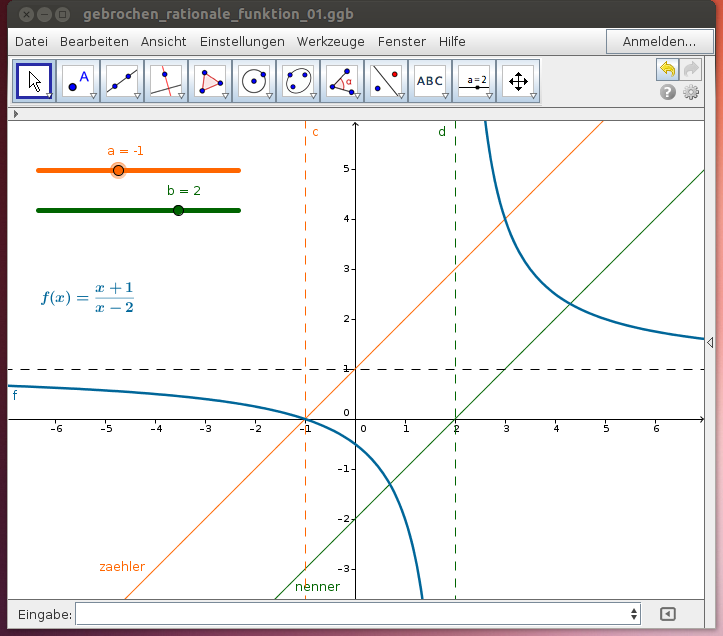
1 Nullstelle des Zählerpolynoms, 1 Nullstelle des Nennerpolynoms
Aufgaben:
- Begründe, warum die gebrochen rationale Funktion genau 1 Nullstelle und genau 1 vertikale Asymptote hat!
- Variiere den Zähler und den Nenner mit Hilfe der Schieberegler und vergleiche die Eigenschaften des Zählerpolynoms und des Nennerpolynoms mit den Eigenschaften der gebrochen rationalen Funktion!
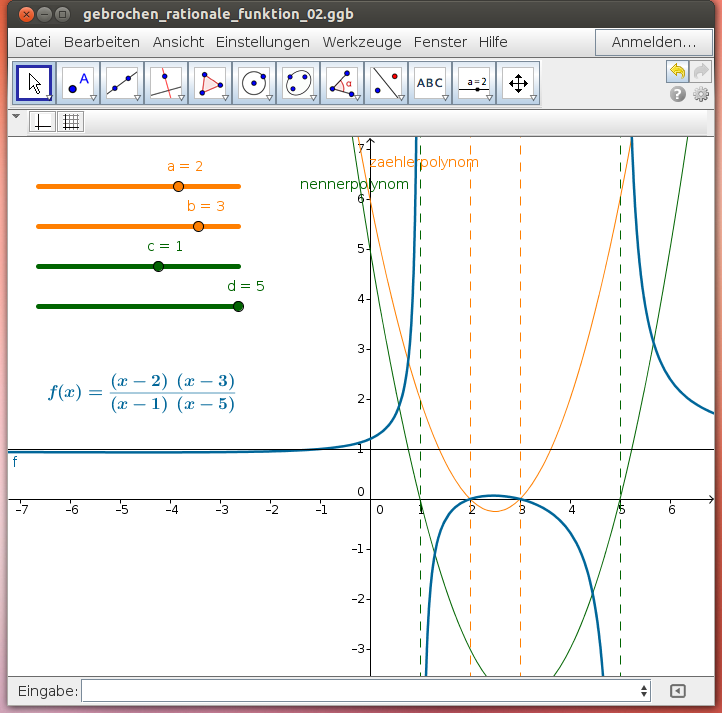
2 Nullstellen des Zählerpolynoms, 2 Nullstellen des Nennerpolynoms
Aufgaben:
- Begründe, warum die gebrochen rationale Funktion genau 2 Nullstellen und genau 2 vertikale Asymptote hat!
- Variiere das Zählerpolynom und das Nennerpolynom mit Hilfe der Schieberegler und vergleiche die Eigenschaften des Zählerpolynoms und des Nennerpolynoms mit den Eigenschaften der gebrochen rationalen Funktion!
- Erstelle weitere gebrochen rationale Funktionen und untersuche ihre Nullstellen und ihre vertikalen Asymptoten!
- Lies aus den Eigenschaften des Zählerpolynoms und des Nennerpolynoms die Gleichung der horizontalen Asympote ab und vergleiche mit der grafischen Darstellung!
Zurück zu Reelle Funktionen