Inhaltsverzeichnis
Thema: Geometrische Örter und Ortslinien
Punkte, die eine bestimmte geometrische Eigenschaft haben, können zu Linien oder Flächen zusammengefasst werden. Sie bilden dann einen „geometrischen Ort“, dessen Punkte alle gleiche Eigenschaften haben.
Einzelne Punkte
Umkreismittelpunkt
Bestimme den Punkt, der von drei gegebenen Punkten A, B unc C den gleichen Abstand hat!
Inkreismittelpunkt
Bestimme den Punkt, der von drei Dreieckseiten den gleichen Normalabstand hat!
Inkreis- und Ankreismittelpunkte
Bestimme die Punkte, die von drei (nicht parallelen) Geraden die gleichen Normalabstände haben!
Strecken und Linien
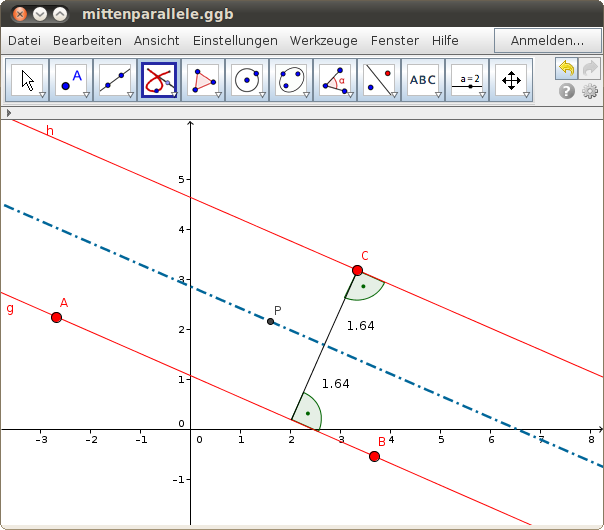
Mittenparallele
Bestimme die Punkte, die von zwei parallelen Geraden g und h den gleichen Abstand haben!
Parallelenpaar
Bestimme die Punkte, die von einer Geraden den gegebenen Normalabstand d haben!
Streckensymmetrale
Bestimme die Punkte, die von zwei gegebenen Punkten A und B gleich weit entfernt sind!
Winkelsymmetrale
Bestimme die Punkte, die von zwei (schneidenden) Geraden g und h den gleichen Normalabstand haben!
Kreislinie
Bestimme die Punkte, die vom Punkt M den Abstand von r LE haben!
Thaleskreis
Bestimme die Punkte, von denen aus eine gegebene Strecke unter einem rechten Winkel erscheint!
Randwinkelbogenpaar
Bestimme die Punkte, von denen aus eine gegebene Strecke unter einem bestimmten Winkel erscheint!
Ellipse
Bestimme die Punkte, für die die Summe ihrer Entfernungen zu zwei gegebenen Brennpunkten F1 und F2 den Wert 2a hat!
Ei-Kurve
Hyperbel
Bestimme die Punkte, für die der Betrat der Differenz ihrer Entfernungen zu zwei gegebenen Brennpunkten F1 und F2 den Wert 2a hat!
Parabel
Bestimme die Punkte, die von einer Geraden l (Leitlinie l) und einem Punkt F (Brennpunkt F) den gleichen Abstand haben!
Parameterkurven
Hinweis: Verwende das GeoGebra-Werkzeug „Ortslinie“, um Ortslinien für Punkte, deren Eigenschaften im Grafikfenster festgelegt wurden.
Zusammengesetzte Aufgaben
- Bestimme die Punkte, die zu zwei schneidenden Geraden den gleichen Normalabstand und vom Punkt M den Abstand r LE haben!
- Bestimme die Punkte, die von zwei Punkten A und B gleich weit entfernt sind, und vom Punkt M den Abstand r LE haben!
Flächen
Streifen
Bestimme die Punkte, die von der Geraden g höchstens den Abstand d haben!
Kreisfläche
Bestimmme die Punkte, die vom Punkt M höchstens r LE weit entfernt sind!
Zurück zu Nichtlineare analytische Geometrie (7. Klasse)