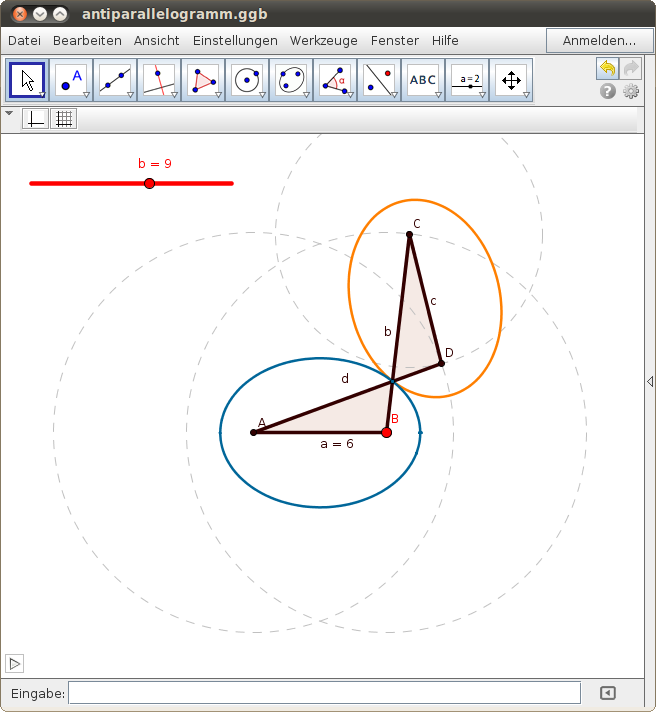
Antiparallelogramm
Gegenüberliegende Seiten eines Antiparallelogramms sind gleich lang, aber nicht parallel: Die beiden längeren Seiten schneiden einander in einem Punkt. Bei fester Basis liegen alle möglichen Schnittpunkte der längeren Seiten auf einer Ellipse:
Aufgaben:
- Lies zum Antiparallelogramm nach (WikiPedia: Antiparallelogramm)!
- Variiere die Basis und die Länge der beiden anderen Seiten des Antiparallelogrammes und beschreibe die Form der Ellipse!
- Die an der Tangente im Schnittpunkt der beiden längeren Seiten gespiegelte Ellipse hat als Brennpunkte die beiden Eckpunkte des Antiparallelogramms, die nicht zur Basis gehören. Begründe!
- Untersuche und vergleiche dazu die Bernoullische Lemniskate!
Zurück zu Nichtlineare analytische Geometrie | Ortslinien