Bernoullische Lemniskate

tm.jpg 7

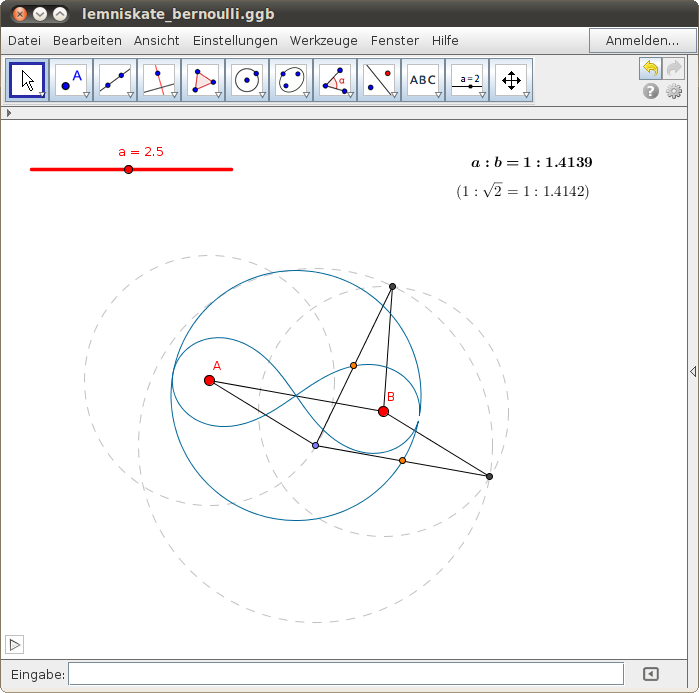
Wir fixieren die längere Seite eines Antiparallelogramms und lassen die anderen Seiten umkreisen. Der Mittelpunkt der beweglichen längeren Seite beschreibt dann eine Lemniskate. Ist das Verhältnis der Seiten tex:1 : \sqrt 2, so entsteht die Bernoullische Lemniskate.

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Lies zur WikiPedia: Lemniskate nach!
  • Wähle im GeoGebra-Beispiel die Länge der kürzeren Seite a mit dem Schieberegler und verschiebe den roten Punkt B (mit den Pfeiltasten) so, dass das Verhältnis der kürzeren zur längeren Seite des Antiparallelogramms tex:1 : \sqrt 2 beträgt!
  • Der Halbierungspunkt der fixierten langen Seite des Antiparallelogramms wird von der Lemniskate zweimal durchlaufen. In ihm schneiden die Tangenten die fixierte Seite unter einem bestimmten Winkel. Bestimme diesen!
  • Beschreibe die Form der Lemniskaten bei „beliebigen“ Werten für a und b! Welche Bereiche für a und b sind dabei überhaupt möglich?

Zurück zu Nichtlineare analytische Geometrie | Ortslinien


Zuletzt angesehen: • exponentialfunktion_32 • harmonische_schwingung • integrale • statistik • bernoullische_lemniskate