Astroide
Die Astroide (Sternkurve) wird im folgenden GeoGebra-Applet auf verschiedene Weise erzeugt und dargestellt:
Parameterkurve
x(t) = 4 cos(t)^3 y(g) = 4 sin(t)^3
(schwarz dargestellte Parameterkurve)
Hypozykloide
x(t) = 3 cos(t) + cos (3t) y(t) = 3 sin(t) - sin (3t)
(rot dargestellte Parameterkurve)
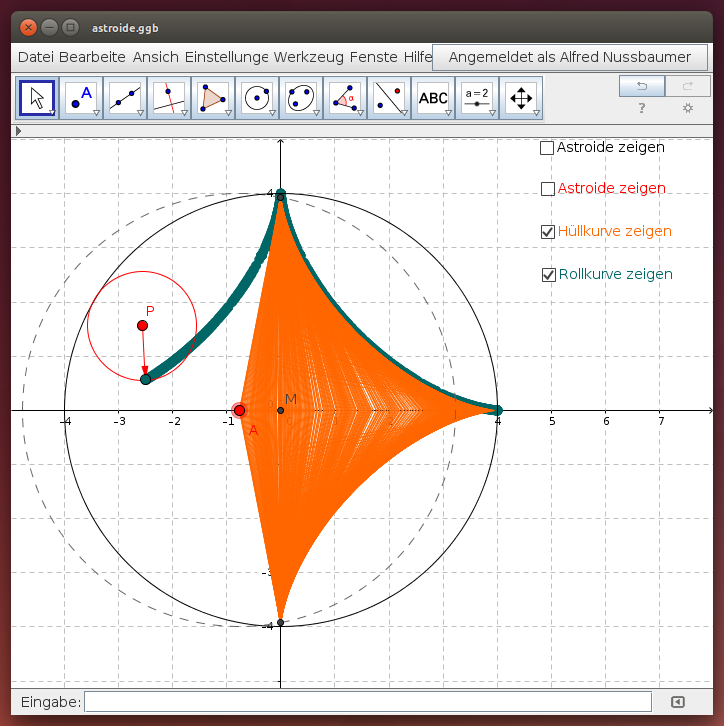
Hüllkurve
Die Endpunkte einer Strecke (l = 4 E) liegen auf der x- und auf der y-Achse. In welcher Entfernung vom Koordinatenursprung kann die Strecke „um die Ecke“ bewegt werden?
(orange Spur der Strecke)
Rollkurve
Ein Kreis mit Radius ri = 1 E rollt innen auf dem Kreis mit Radius ra = 4 E ab. Beobachte die Bahn eines Punkts auf dem Umfang des inneren Kreises!
(Spur des Punktes)
Wähle im folgenden GeoGebra-Applet die gewünschte Darstellungsform und stelle die Astroide dar. Bewege dazu entweder den Punkt A oder den Punkt P:
Aufgaben:
- Vergleiche die beiden Parameterdarstellungen und prüfe nach, dass es sich um die gleiche Kurve handelt!
- Formuliere folgende Aufgabe: Ein Gemälde mit der Breite b soll in einem engen, rechtwinklig abzweigenden Gang transportiert werden …
- Vergleiche allgemein mit Hüllkurven!
- Vergleiche mit der Parameterdarstellung der Zykloide!
Weitere Beispiele: Ellipse | Hyperbel | Parabel | Astroide | Katakaustik | Katakaustik und Kardioide
Zurück zu Parametrisierte Kurven | Ortslinien