| Zurück zu: 5.Klasse » Analytische Geometrie der Ebene |
Inkreismittelpunkt
(zu 
- Einstieg in die Oberstufe, S. 18 - 19)
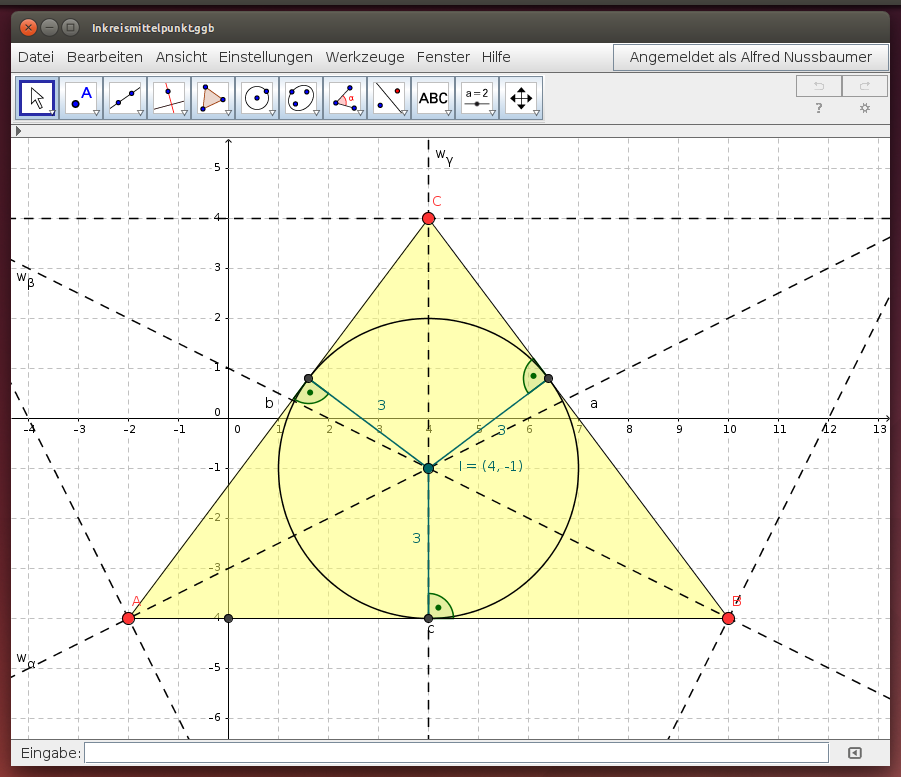
Die drei Winkelsymmetralen des Dreiecks schneiden einander in einem Punkt, dem Inkreismittelpunkt.
- Der Inkreismittelpunkt ist von allen drei Dreieckseiten gleich weit entfernt.
Das folgende GeoGebra-Beispiel eignet sich auch zur Kontrolle von Rechenaufgaben oder zum Finden von „passenden Angaben“:
Hinweis: Du erhältst den Inkreisradius r, indem du vom Inkreismittelpunkt I das Lot (die Normale) auf eine Dreiecksseite legst. Die Entfernung vom Lotfußpunkt zum Inkreismittelpunkt legt den Inkreisradius fest.
Anmerkung: Ist der Umkreisradius und
der Inkreisradius, dann gilt für die Entfernung
zwischen dem Inkreismittelpunkt I und dem Umkreismittelpunkt U:
- Überprüfe dies an Hand einer geeigneten GeoGebra-Zeichnung!
Anmerkung: Die drei Ankreise berühren jeweils eine Dreieckseite „von außen“ und die Verlängerungen der beiden anderen Dreieckseiten. Du findest die Mittelpunkte dieser Ankreise als Schnittpunkte der Normalen auf die Winkelsymmetralen des Dreiecks.
Vergleiche mit der Konstruktion von Schwerpunkt, Höhenschnittpunkt und Umkreismittelpunkt.
Zurück zu Analytische Geometrie der Ebene
