Kreis und Kreisgleichung

(zu tm.jpg, 7)

Betrachte einen Kreis, dessen Mittelpunkt M im Koordinatenursprung liegt: M(0|0). Alle Punkte P(x|y) auf der Kreislinie sind vom Mittelpunkt M gleich weit entfernt: tex:\overline{MP} = r, tex:\vert \vec {MP} \vert = r.

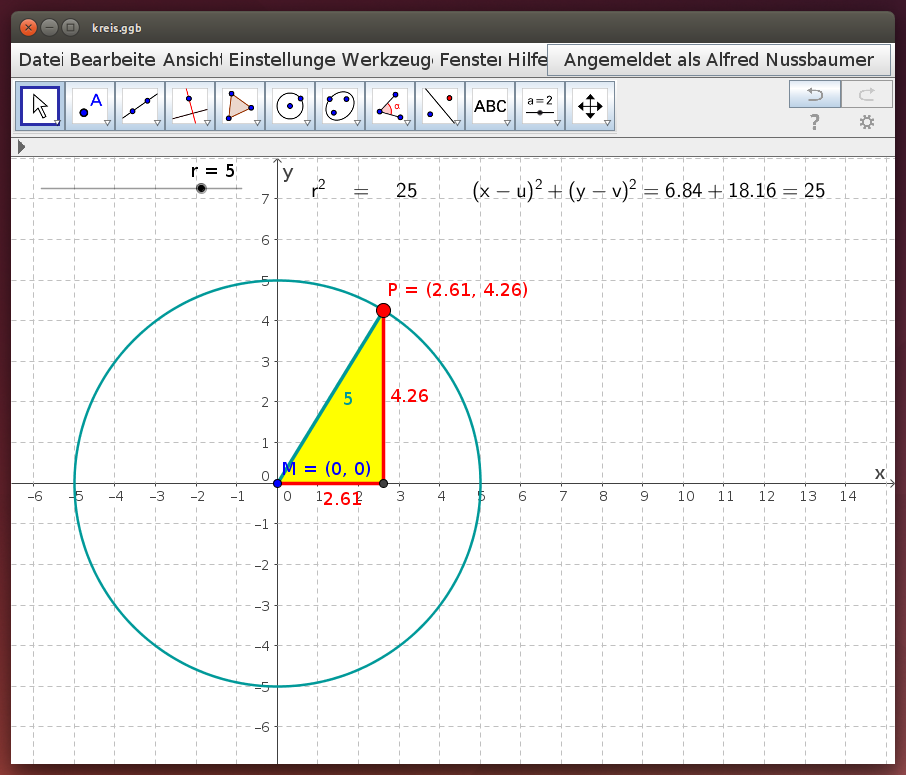
Untersuche im folgenden GeoGebra-Applet für verschiedenen Punkte P jeweils das rechtwinklige Dreieck, das aus den Koordinatenabschnitten x und y und aus dem Radius r gebildet wird:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Wiederhole die Herleitung der Kreisgleichung tex:k: x^2 + y^2 = r^2 !
  • Verschiebe den Mittelpunkt M im obigen GeoGebra-Applet, verschiebe den Punkt P auf der Kreislinie und beobachte die angegebene Gleichung!
  • Wiederhole die Herleitung der Kreisgleichung tex:k: (x-u)^2 + (y-v)^2 = r^2 (Mittelpunkt M(u|v))!

Parameterdarstellung

Für alle Punkte tex:P(r \cdot cos(t) | r \cdot sin(t)) auf der Kreislinie gilt die tex:x^2 + y^2 = (r \cdot cos(t))^2 + (r \cdot sin(t))^2 = r^2 \cdot (cos(t)^2 + sin(t)^2)) = r^2. Mit dem Parameter t kann die Position eines Punktes P auf der Kreislinie beschrieben werden.

Lies den Artikel zu parametrisierte Kurven!

Zurück zu Nichtlineare analytische Geometrie R2


Zuletzt angesehen: • kreis