Inhaltsverzeichnis

Lernpfad Polynomfunktionen

(zu tm.jpg 7)

Dieser Lernpfad behandelt zunächst einige bekannte Eigenschaften von Polynomfunktionen. Die Bedeutung der Schnittpunkte mit der x-Achse („Nullstellen“) und die Bedeutung des Durchstoßpunktes durch die y-Achse („Anfangswert“) stellt eine Wiederholung des Wissens aus der 5. und 6. Klasse dar.

In den nächsten Schritten lernst du die Bedeutung der 1. und 2. Ableitung der Polynomfunktion kennen und berechnest Hoch-, Tief- und Wendepunkte.

Den Abschluss bilden die Kurvendiskussion, Umkehraufgaben und einige Extremwertsaufgaben mit Polynomfunktionen.

Hinweis: Viele Lern- und Rechenschritte kannst du auf alle Funktionenfamilien übertragen!

Grundlagen

Multipliziere Potenzfunktionen (mit verschiedenen Hochzahlen) mit Koeffizienten und bilde die Summe. Du erhältst eine Polynomfunktion, zB:

tex:f(x) = x^3 + 4x^2 - 1 (eine Polynomfunktion 3. Grades)

tex:f(x) = x^4 + 4x^2 + 1 (eine Polynomfunktion 4. Grades)

tex:f(x) = 7x^5 + 4x^3 (eine Polynomfunktion 5. Grades)

…

Beachte, dass wir bei allen Beispielen die Potenzfunktionen nach fallenden Hochzahlen geordnet haben. Der Grad der Polynomfunktion (die höchste vorkommende Hochzahl) ist dann einfach die Hochzahl des ersten Summanden.

Allgemein: tex:f(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + ... + a_1 x + a_0 ist eine Polynomfunktion n-ten Grades.

Nullstellen einer Polynomfunktion, Durchstoßpunkt durch die y-Achse

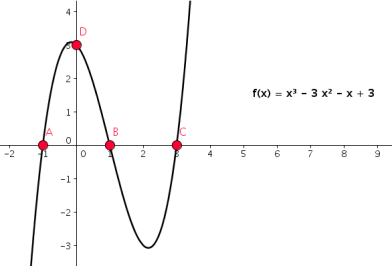
Polynomfunktionen können durch verschiedene Eigenschaften festgelegt werden. In der folgenden Abbildung wird die Polynomfunktion 3. Grades durch 3 Nullstellen (Punkte A, B, C) und durch den Durchstoßpunkt durch die y-Achse (Punkt D) festgelegt:

Grafik: Alfred Nussbaumer

Vergleiche auch: Quadratische Funktion wird durch 2 Nullstellen und einen Durchstoßpunkt durch die y-Achse festgelegt

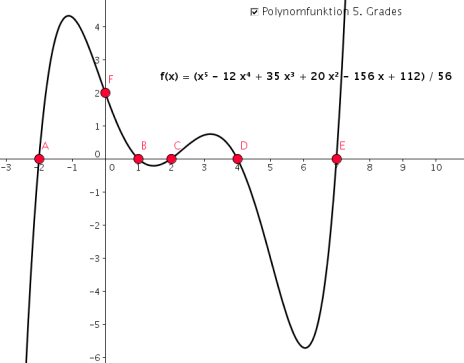
Im folgenden Beispiel wird eine Polynomfunktion 5. Grades durch 5 Nullstellen (Punkte A, B, C, D, E) und durch den Durchstoßpunkt durch die y-Achse (Punkt F) festgelegt:

Grafik: Alfred Nussbaumer

Außer dem Durchstoßpunkt durch die y-Achse, und noch dazu, wenn eine Funktion weniger oder gar keine Nullstellen besitzt, können Polynomfunktionen durch besondere Punkte beschrieben und festgelegt werden. Eine besondere Rolle dabei spielen „Scheitelpunkte“, die wir besser als Maxima (Hochpunkte) und Minima (Tiefpunkte) bezeichnen. Vergleiche dazu die Beschreibung einer quadratischen Funktion:

Bei Hoch- und Tiefpunkten ändert sich jeweils die Monotonie einer Funktion. Punkte, in denen sich die Krümmung einer Funktion ändert, Wendepunkte, eigenen sich ebenso, Funktionen festzulegen. Sowohl die Monotonie als auch die Krümmung lassen sich mit Hilfe der Ableitungsfunktionen gut untersuchen.

Ableitung der Polynomfunktion

Wiederhole die Ableitungsregeln:

Bilde die erste und die zweite Ableitung:

Untersuche den Zusammenhang zwischen dem Funktionsgraphen und den Graphen der 1. Ableitung und der 2. Ableitung:

Eigenschaften von Polynomfunktionen

Extremwertaufgaben, Optimierung

Zurück zu Differentialrechnung