Extremwertaufgabe (Rechteck)
Der Flächeninhalt eines Rechtecks ist gegeben. Variiere die Länge a des Rechtecks, indem du den Punkt B verschiebst und beobachte den Umfang des Rechtecks - für welche Abmessungen ist der Umfang am kleinsten?
Der Umfang u ist eine Funktion dieser Länge a, ihr Graph entsteht als Punktespur.
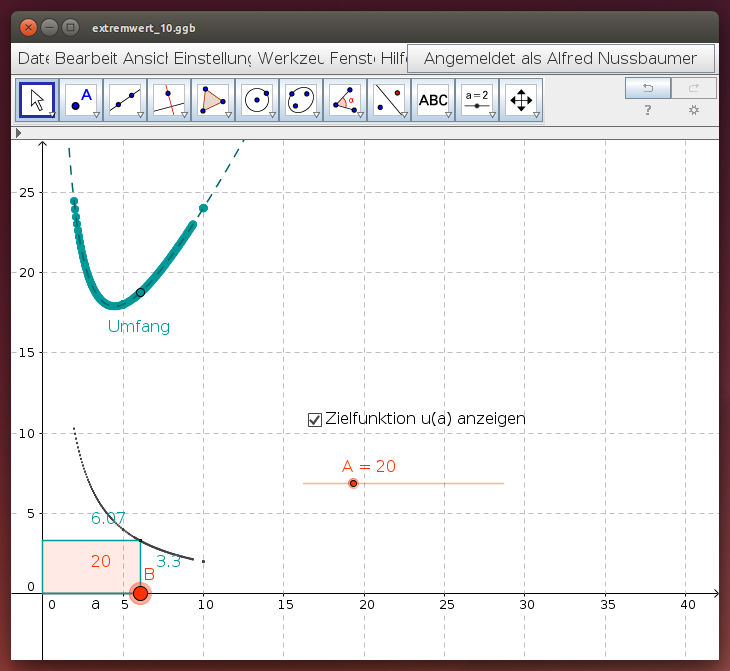
Aufgaben:
- Für welche Länge a wird der Umfang u(a) am kleinsten? Lies die Abmessungen des Rechtecks und seinen Umfang aus der Grafik ab!
- Wähle mit dem Schieberegler für A andere Flächeninhalte, z.B. A = 25 E2 und bestimme das Rechteck mit dem geringsten Umfang (Tipp: Mit Strg F löschst du die Spur).
- Beschreibe die Form des Rechtecks, wenn du eine Lösung für den kleinsten Umfang gefunden hast. Liegt ein besonderes Rechteck vor?
- Löse die Aufgabe mit Hilfe einer Tabelle!
- Löse die Aufgabe rechnerisch mit Hilfe der Zielfunktion u(a) und ihren Ableitungen. Vergleiche mit der grafischen Lösung!
Zurück zu Anwendungen der Differentialrechnung | Extremwertaufgaben | Ebene Aufgaben | Thema Polynomfunktionen
