Die Ableitungsfunktion
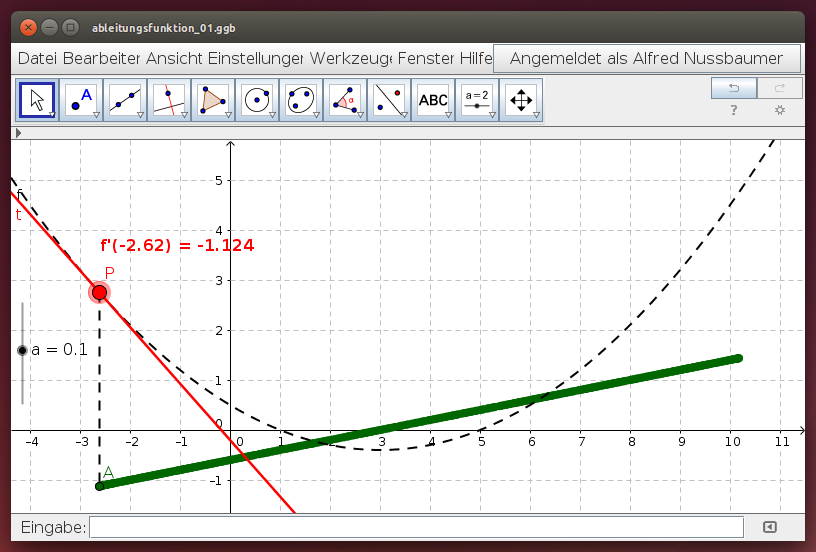
Wir können die Tangente zu jedem Punkt einer Funktion darstellen. Ihre Steigung hängt jeweils von der Position des Berührungspunkts (und von der Funktion f) ab. In der Ableitungsfunktion können wir dies für alle Punkte der gegebenen Funktion darstellen.
Verschiebe den Berührpunkt P und beobachte die Spur von Punkt A:
Aufgaben:
- Die Spur von A bildet selbst eine Funktion. Beschreibe, um welche Funktion es sich im obigen Beispiel handelt!
- Wähle verschieden „steile“ Funktionen
mit dem Schieberegler für a und beschreibe, wie sich dadurch die Ableitungsfunktion ändert (Tipp: Mit <Strg> F löschst du die Spur des Punktes A).
- Untersuche genau, in welchem Punkt der Funktion f das Verhalten der Monotonie wechselt (die Monotonie wechselt von „streng monoton fallend“ nach „streng monoton steigend“): In welchem Punkt ist dies der Fall? Welche besondere Lage hat die Tangente in diesem Punkt?
Zurück zu Polynomfunktionen | Monotonie