(zu 7)

• Oberfläche eines quadratischen Prismas bei gegebenem Volumen

• Oberfläche eines Zylinders bei gegebenem Volumen

• Nullstellen, Hoch- und Tiefpunkte, Wendestellen

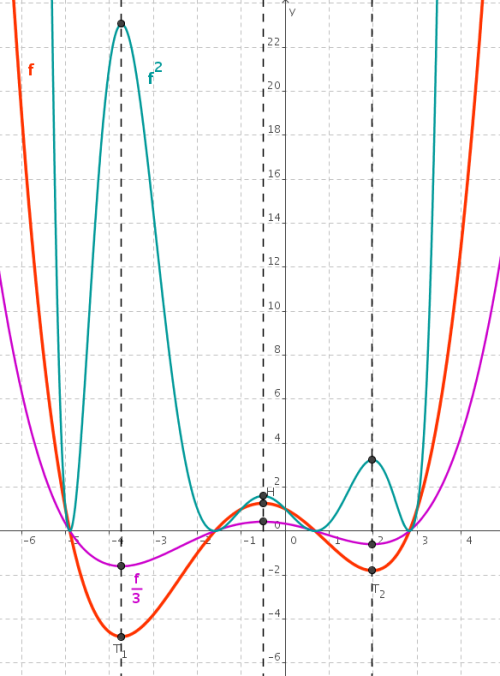
In der Abbildung sind die Zielfunktion f, f / 3 und ihr Quadrat f² dargestellt. Beachte, dass die Stellen, an denen Extremwerte auftreten, dabei gleich bleiben!

Hinweis: Bildest du das Quadrat der Funktion, so wird aus einem Tiefpunkt der Funktion f ein Hochpunkt von f².

Die Nullstellen der Funktion bilden die Tiefpunkte von f².

Extremwertaufgabe - Vereinfachung der Zielfunktion (vgl. 7):

1. Vereinfachung der Zielfunktion: Die Stellen von Hoch- und Tiefpunkten bleiben unverändert, wenn du die Zielfunktion durch eine Konstante dividierst.

2. Vereinfachung der Zielfunktion: Die Stellen von Hoch- und Tiefpunkten bleiben unverändert, wenn du die Zielfunktion quadrierst.

Beachte, dass dem Tiefpunkt der Funktion f ein Hochpunkt der Funktion f² entspricht.

• Wie groß ist das größte Rechteck, das du mit einem Seil gegebener Länge in der Ecke des Schulhofes abtrennen kannst?
• Finde das Rechteck, das bei gegebenem Flächeninhalt den kleinsten Umfang hat!
• Von einer rechteckigen Glasplatte wurde eine Ecke geradlinig abgetrennt. Berechne, welches flächengrößte Rechteck man aus der Glasplatte ausschneiden kann!
• Welcher Punkt der Kurve hat den kürzesten Abstand vom Koordinatenursprung?
• Welchen senkrechten Abstand haben zwei Kurven miteinander ... ?

• Ein Trichter hat die Gestalt einer auf dem Kopf stehenden quadratischen Pyramide (ohne Basisfläche). Wie ist er bei einer gegebenen Oberfläche zu dimensionieren, damit sein Volumen maximal wird?

• Von welchem Punkt aus ist die Summe aller Verbindungen zu allen Punkten der Fläche am kleinsten (zur Aufgabe)?

Zurück zu Anwendungen der Differentialrechnung | Thema: Polynomfunktionen