Die Ableitungsfunktion der Ableitungsfunktion: Die 2. Ableitung
Wir können die Tangente zu jedem Punkt einer Funktion darstellen. Ihre Steigung hängt jeweils von der Position des Berührungspunkts (und von der Funktion f) ab. Damit erhalten wir die 1. Ableitung. Nun untersuchen wir die Ableitung der 1. Ableitung: Die Steigung der Tangente in Punkt A legt Punkt für Punkt eine neue Funktion fest, die du als Spur im folgenden GeoGebra-Applet sehen kannst:
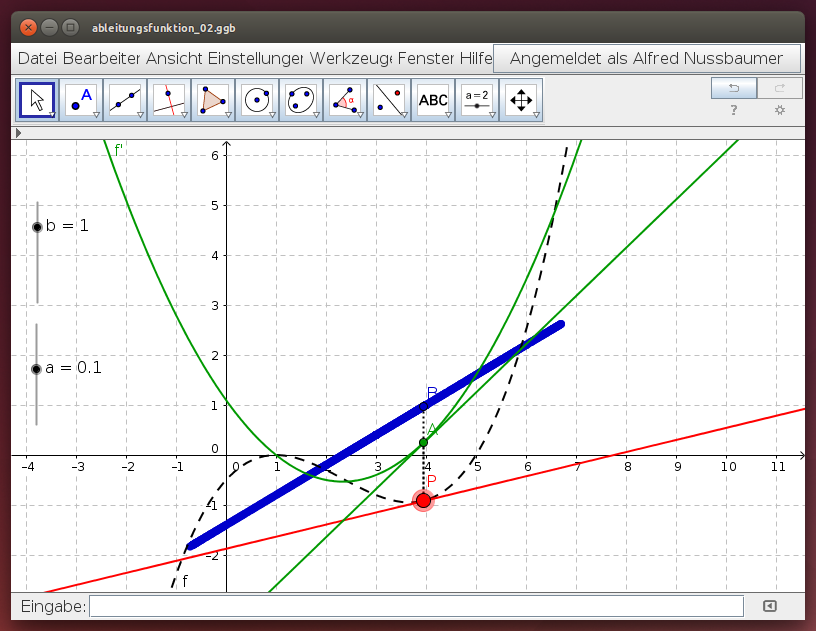
Verschiebe den Punkt P auf dem Funktionsgraphen von f, beobachte die Tangentensteigung im zugehörigen Punkt A und die Position des Punktes B:
Aufgaben:
- Vergleiche die Eigenschaften der Ableitungsfunktion f'(x) (und die jeweilige Tangente von A in f'(x)) mit der Position des Punktes B: Wann liegt B unterhalb der x-Achse, wann oberhalb?
- Vergleiche die Eigenschaften der Funktion f mit der Position des Punktes B: Wann liegt die Funktion f in der Nähe zu Punkt P unterhalb der Tangente in P und wann oberhalb?
- Die Spur des Punktes P beschreibt die Ableitung der Funktion f'(x). Überprüfe dies!
- Die 2. Ableitung ist die Ableitung der 1. Ableitung. Sie beschreibt das Monotonieverhalten der 1. Ableitung.
- Die 2. Ableitung beschreibt das Krümmungsverhalten der Funktion f.
Wir legen fest:
f ist in P(x|f(x)) positiv gekrümmt (in der Nähe des Punktes P liegt der Funktionsgraph oberhalb der Tangente in P).
f ist in P(x|f(x)) negativ gekrümmt (in der Nähe des Punktes P liegt der Funktionsgraph unterhalb der Tangente in P).
Zurück zu Polynomfunktionen | Monotonie | Krümmung