Hochpunkte
7, S. 114 - 115
Ein Hochpunkt ist ein lokales oder globales Maximum der Funktion f (vgl. 
).
).
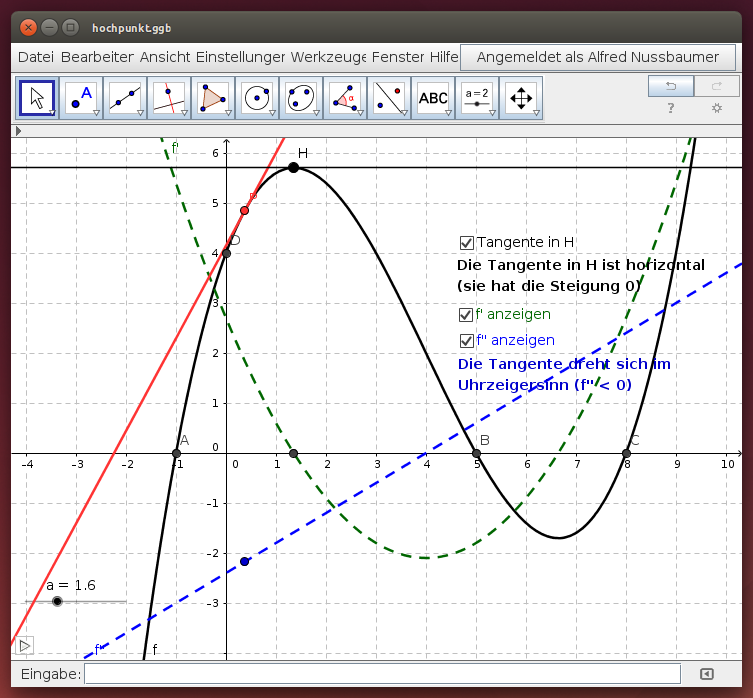
Im folgenden GeoGebra-Applet wandert der Punkt P auf dem Funktionsgraphen von f. Starte dazu die Animation mit dem 
- Icon, das sich in der linken unteren Ecke des Applets befindet.
Beobachte die Lage der Tangente in P:
Aufgaben:
- Beschreibe die Lage der Tangente in der Nähe des Hochpunktes H!
- Nenne Argumente dafür, dass der Hochpunkt H im Vergleich zu allen weiteren Punkten in seiner unmittelbaren Nähe den größten Funktionswert hat!
- Beweise: Wäre die Tangente in H nicht horizontal, dann könnte H nicht den größten Funktionswert (im Vergleich zu allen weiteren Punkten in seiner unmittelbaren Nähe) haben.
- Die Punktespur stellt die 2. Ableitung der Funktion dar. Gib Gründe dafür an, dass alle diese Werte negativ sind (Hinweis: Untersuche die Eigenschaften der 1. Ableitung).
zurück zu Polynomfunktionen | Eigenschaften von Funktionen | Tiefpunkte | AN3.3
