Krümmung
Die Krümmung einer Funktion beschreibt, wie sie „ihre Richtung ändert“, wenn sie von links nach rechts durchlaufen wird. Genau genommen, dreht sich die Tangente in einem Punkt des Funktionsgraphen, wenn der Punkt P von links nach rechts verschoben wird.
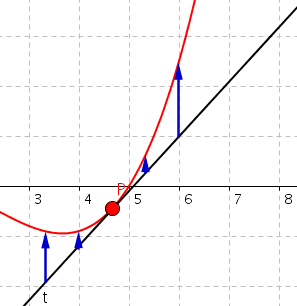
So kannst du aus der folgdenen Abbildung ablesen, dass die Funktion eine positive Krümmung hat: Die Tangente dreht sich gegen den Uhrzeigersinn, wenn der Punkt P von links nach rechts verschoben wird:
In diesem Fall gilt: Alle Punkte der Funktion liegen oberhalb der Tangente in P.
Aufgabe:
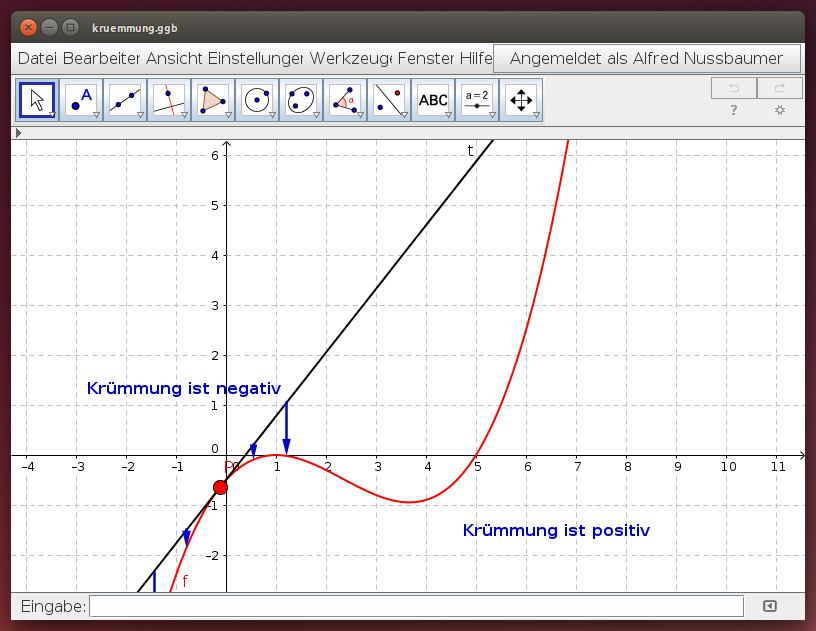
Verschiebe den Punkt P von links nach rechts und beobachte, wie sich die Tangente in P dreht:
- Beschreibe ungefähr, in welchem Bereich die Funktion negativ, und in welchem Bereich sie positiv gekrümmt ist!
- Ungefähr an welcher Stelle ändert die Krümmung der Funktion ihr Vorzeichen?
- Die Funktion ist in einem Bereich negativ gekrümmt und in einem Bereich positiv gekrümmt. Beschreibe, wie dies mit dem Vorzeichen der 2. Ableitung der Funktion zusammenhängt!
f(x) ist negativ gekrümmt
f(x) ist positiv gekrümmt
Untersuche, wie die Krümmung einer Funktion mit dem Vorzeichen ihrer 2. Ableitung zusammenhängt:
Zurück zu Polynomfunktionen | AN3.3