Monotonie

7, S. 114 - 115

Die Monotonie einer Funktion (oder einer Folge) gibt, ob die Werte bei zunehmendem Argument x (oder n) stets zu- oder abnehmen.

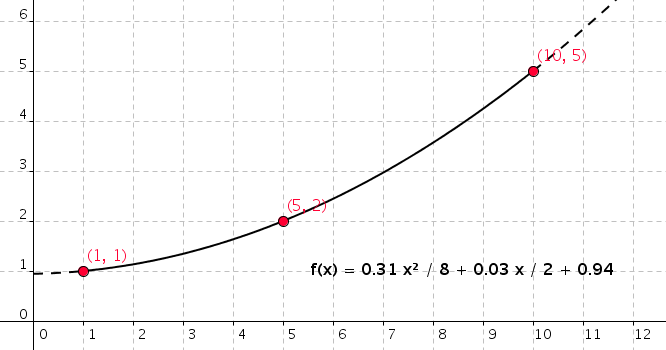
So lässt sich für die in der folgenden Abbildung dargestellten Funktion sicher sagen, dass sie im Intervall [1;5] streng monoton steigt:

Eine Funktion f heißt streng monoton steigend in einem Intervall [a;b], wenn für alle Zahlen $tex:x_1, x_2 \in [a;b]$ gilt: $tex:x_1 < x_2 \Rightarrow f(x_1) < f(x_2)$
Eine Funktion f heißt monoton steigend in einem Intervall [a;b], wenn für alle Zahlen $tex:x_1, x_2 \in [a;b]$ gilt: $tex:x_1 < x_2 \rightarrow f(x_1) \le f(x_2)$

Analog legen wir fest, wann eine Funktion streng monoton fallend oder monoton fallend heißt (vgl. 7).

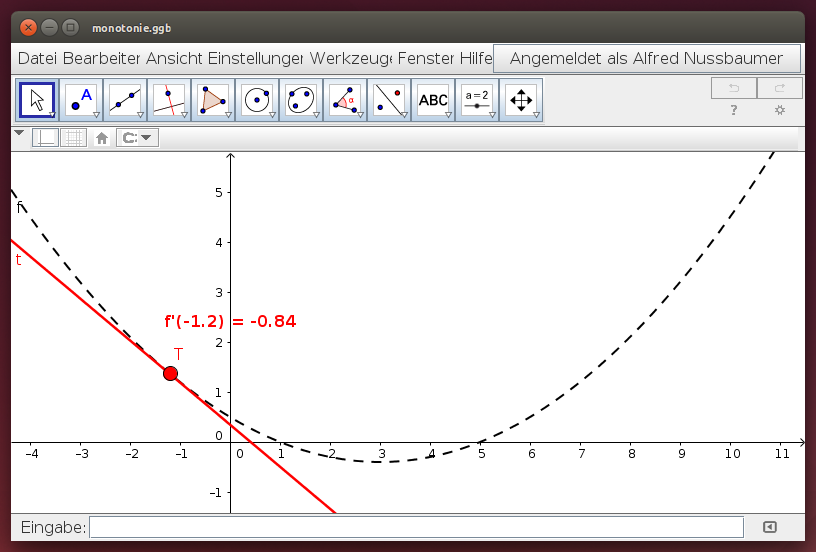
Untersuche die Monotonie der Funktion und vergleiche jeweils mit der Steigung der Tangente!

Die Funktion ist in einem Bereich streng monoton fallend und in einem anderen streng monoton steigend. Beschreibe genau den Zusammenhang zwischen dieser Monotonie und dem Vorzeichen der Tangentensteigung!
Die Funktion f(x) ist in einem Bereich streng monoton fallend und in einem anderen streng monoton steigend. Beschreibe genau den Zusammenhang zwischen dieser Monotonie und dem Vorzeichen der 1. Ableitung, f'(x)!

Eine Funktion f heißt streng monoton steigend in einem Intervall [a;b], wenn für alle Zahlen $tex:x \in [a;b]$ gilt:
Eine Funktion f heißt monoton steigend in einem Intervall [a;b], wenn für alle Zahlen $tex:x \in [a;b]$ gilt: $tex:f'(x) \ge 0$

Analog legen wir fest, wann eine Funktion streng monoton fallend oder monoton fallend heißt (vgl. 7).

Untersuche wie das Monotonieverhalten einer Funktion von der ersten Ableitung abhängt:

Zuletzt angesehen: • monotonie