Nullstellen und Polynomfunktionen
(zu  5, Thema Funktionen)
5, Thema Funktionen)
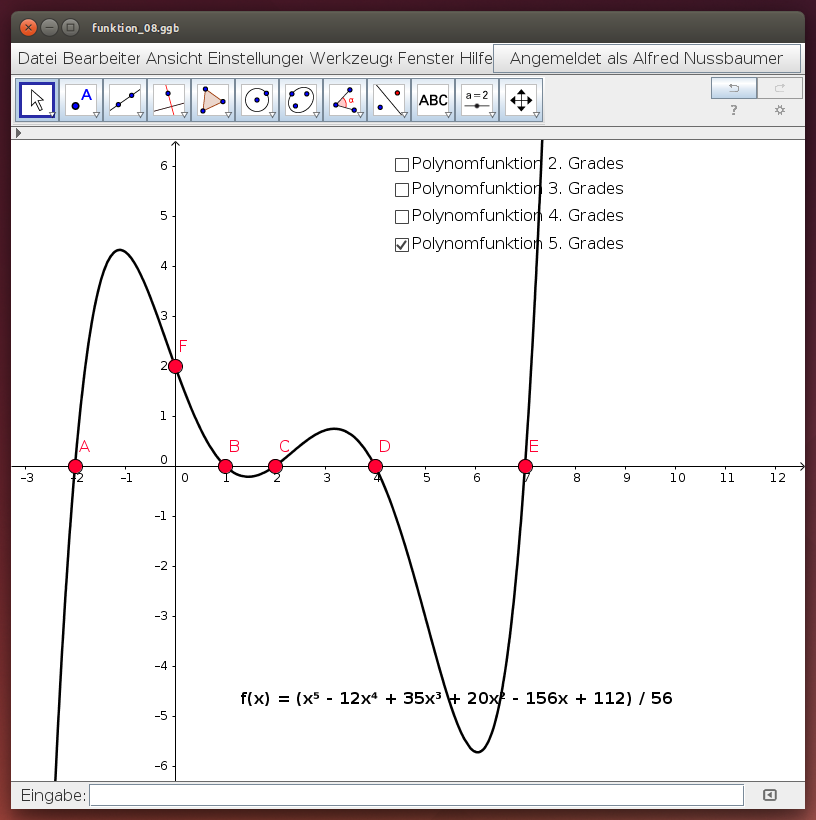
Eine Funktion mit der Gleichung ist eine Polynomfunktion 5. Grades: Es treten nur ganzzahlige, positive Exponenten auf, und der größte Exponent ist 5. Solche Funktionen können bis zu fünf verschiedene Nullstellen (Schnittpunkte mit der x-Achse) haben.
Wähle im folgenden GeoGebra-Beispiel zunächst den Grad der Polynomfunktion aus und untersuche anschließend, wie ihre Form von der Wahl der Nullstellen und des Durchstoßpunkts F durch die y-Achse abhängt!
Aufgaben:
- Untersuche, wie die Lage der Nullstellen zueinander die Form des Funktionsgraphen beeinflussen!
- Kommen zwei Nullstellen aufeinander zu liegen, sprechen wir von einer Doppel-Nullstelle. Was bewirkt das für die Gestalt des Funktionsgraphen?
- Welche Eigenschaften hat der Funktionsgraph in der Nähe einer dreifachen Nullstelle?
- Untersuche symmetrische Funktionsgraphen: Teile dazu eine gerade Anzahl von Nullstellen symmetrisch zum Koordinatenursprung auf!
- Untersuche und beschreibe, welche Wahl der Nullstellen keine Lösung ergibt!
Zurück zu Funktionen