Inhaltsverzeichnis
Lernpfad GeoGebra: Parametrisierte Kurven
- 7, Themenheft Mathematik mit GeoGebra
Bei diesem Lernpfad erarbeitest du ebene Kurven und Raumkurven, die jeweils durch Parameter dargestellt werden. Ausgehend von der Parameterdarstellung der Geraden in der Ebene lernst du, wie du Funktionen und Kurven mit jeweils einem Parameter t festlegen kannst. In der Ebene legst du die Kurven mit Hilfe der beiden Koordinatenfunktionen x(t) und y(t) fest.
Im zweiten Teil arbeitest du mit Raumkurven - du legst sie mit den drei Koordinatenfunktionen x(t), y(t) und z(t) fest.
Du erhältst parametrisierte Kurven, wenn du zwei Funktionen x(t) und y(t) wählst und für jeden Wert t aus einem Intervall [a,b] den Punkt P[x(t)|y(t)] in der Koordinatenebene darstellst. Insbesondere kannst du jeden Funktionsgraph y = f(x) als parametrisierte Kurve [t, f(t)] darstellen.
Die Darstellung von ebenen Kurven ist mit GeoGebra möglich. Raumkurven stellen wir derzeit beispielsweise mit maxima dar.
Geradengleichung
(Strecke)
x(t) = 3 + 2t y(t) = 5 + 3t
Die Kurve [3 + 2t, 5 + 3t] beschreibt für t aus [-2,2] eine Strecke von [-1|-1] bis [7|11] (rechne nach!).
Nichtlineare Funktionen
Parabel
x(t) = t y(t) = a t^2
Hyperbel
x(t) = t y(t) = a / t
Nichtlineare Kurven
Hier lernst du Kurven kennen, bei denen der „Vertikaltest“ versagt - zu einem x kann es mehrere zugehörige y-Koordinaten geben…
Kreis
Ellipse
x(t) = a cos(t) y(t) = b sin(t)
Hyperbel
x(t) = a cosh(t) y(t) = b sinh(t)
Weitere Kurven in Parameterform
Beachte auch, wie du Zykloiden, Rosetten und Spiralen in Polardarstellung, angeben und zeichnen kannst!
Aufgaben:
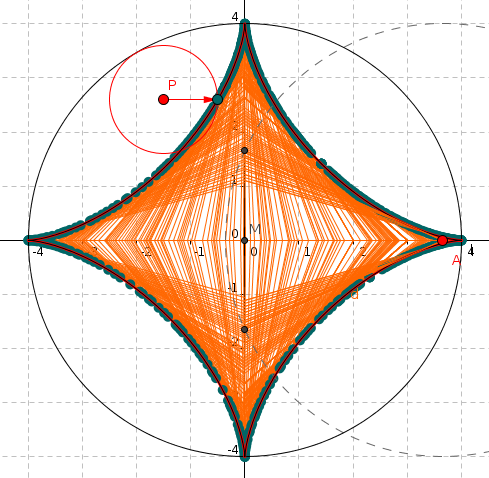
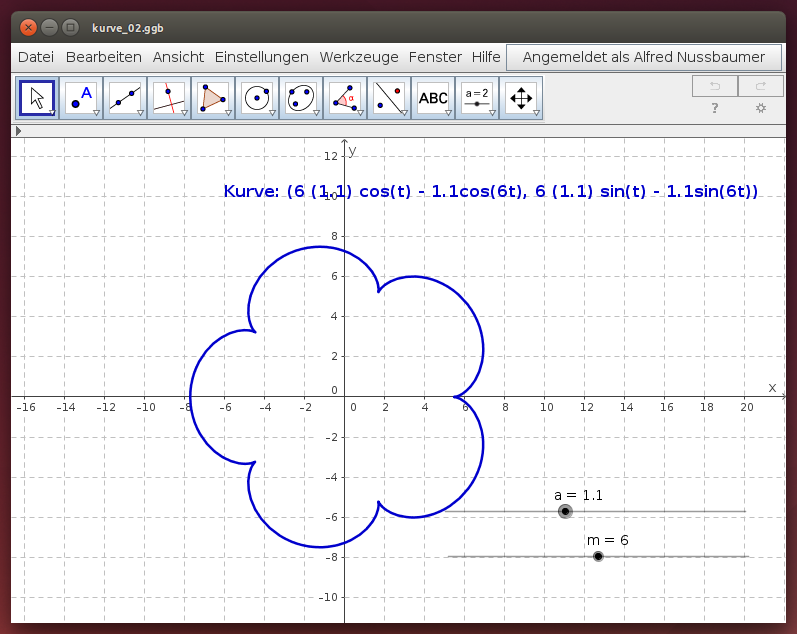
Untersuche die folgenden parametrisierten Kurven mit Hilfe des folgenden GeoGebra-Applets. Gib die Definition der Kurve in er Algebrazeile in der Form Kurve[x(t),y(t),t,0,6.29] ein und verwende auch die Schieberegler für a und m:
- Technologie: Öffne das GeoGebra-Applet und ergänze weitere Schieberegler!
Raumkurven
Erinnere dich an die Parameterdarstellung der Geraden im Raum. Schreibst du die Gleichung in allen drei Koordinaten an, so erhältst du besipielsweise:
x(t) = 1 - 2 t y(t) = 7 + t z(t) = 3 t
Mit geeignet gewählten Funktionen für x(t), y(t) und z(t) erhältst du eine Fülle von Kurven im R3:
- Darstellung von Raumkurven (GeoGebra)
- Darstellung von Raumkurven (Maxima)
Vergleiche die Darstellung von Raumkurven auch mit der Darstellung von Flächen!
Die Polardarstellung erlaubt in vielen Fällen eine einfache und übersichtliche Beschreibung von parametrisierten Kurven und Flächen.
