Inhaltsverzeichnis
Maxima: plot3d (Lernpfad)
(zu  Themenheft Mathematik mit GeoGebra)
Themenheft Mathematik mit GeoGebra)
In diesem Lernpfad lernst du, Funktionen dreidimensional mit Hilfe des Computer-Algebra-Systems Maxima grafisch darzustellen. Darüber hinaus erlaubt dir dieses Werkzeug eine Reihe eigener Entdeckungen …
Funktionen in zwei Variablen
Der Graph einer Funktion in zwei Variablen ist im Allgemeinen eine Fläche im Raum: . Für die folgenden Darstellungen mit Maxima sind neben dem Funktionsterm zumindest die Intervalle für die Variablen x und y anzugeben.
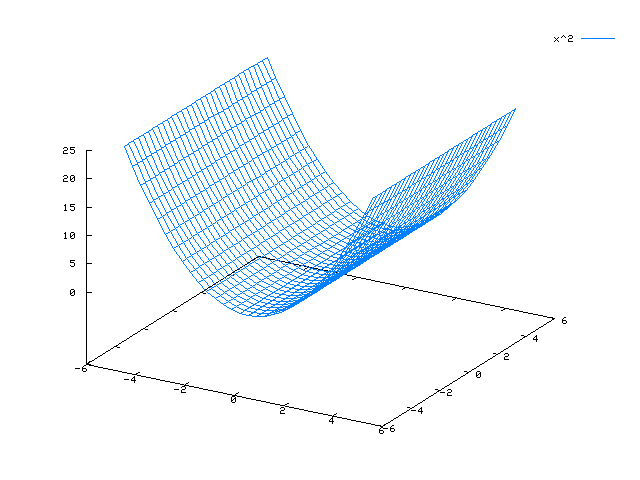
Beispiel: f(x,y) = x^2
Aufgaben:
Untersuche die Funktionsgraphen und erläutere, wie die Fläche von den Variablen abhängt / abhängen könnte!
Hinweis: Wähle geeignete Intervalle für die Variablen x und y!
Kurven und Flächen im Raum (Parameterdarstellung)
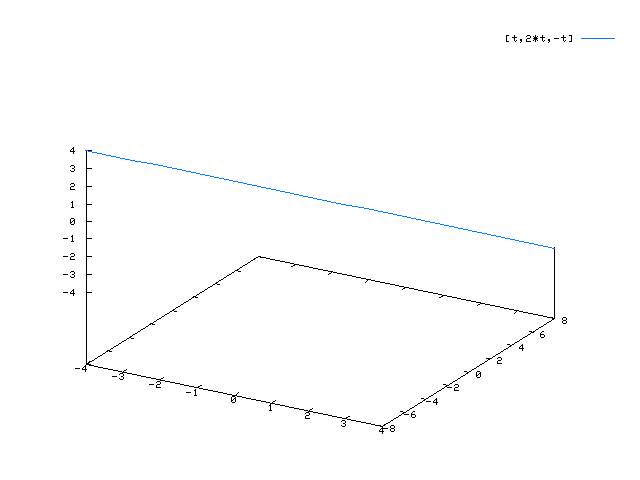
Geraden
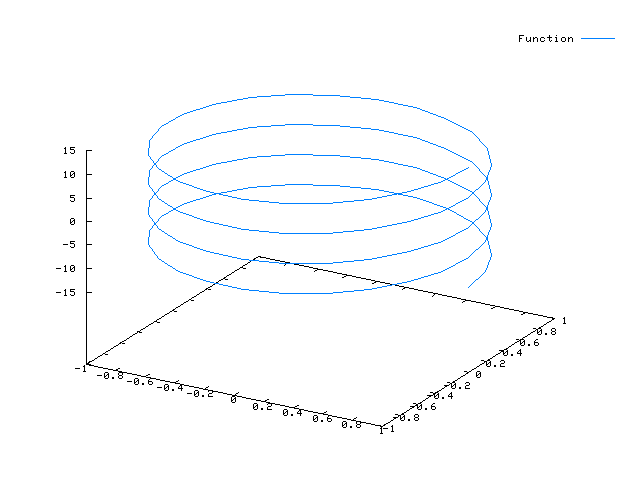
Helix (Schraubenlinie)
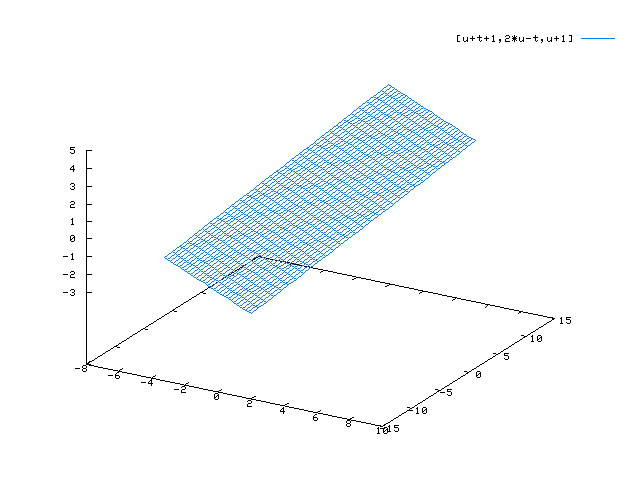
Ebenen
Aufgaben:
- Lies im Artikel Kurven und Flächen im Raum nach!
Ausgabe
Verwende für die Darstellung und Ausgabe einer Grafik (mit gnuplot) verschiedene Parameter:
'grid
Legt die Anzahl der Gitterpunkte für die Variablen fest, z.B.:
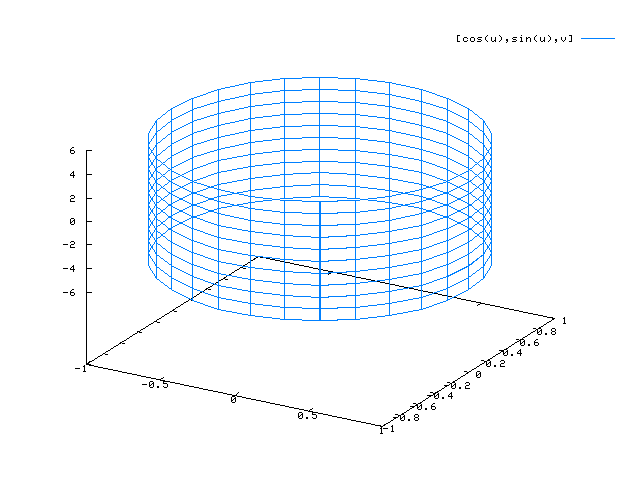
plot3d([cos(u),sin(u),v],[u,0,4*%pi],[v,-5,5], ['grid,60,10]);
Hinweis: Der Vorgabewert für 'grid ist ['grid, 30, 30]
In diesem Fall werden die „Kreise“ aufgrund der 60 Gitterpunkte sehr glatt dargestellt, während in der Richtung des Parameters v (z-Koordinate) nur 10 Gitterpunkte berücksichtigt werden.
gnuplot_pm3d
Lädt erweiterte GNUPLOT-Grafikfunktionen, zB. die Darstellung von Konturen oder farbigen Flächen.
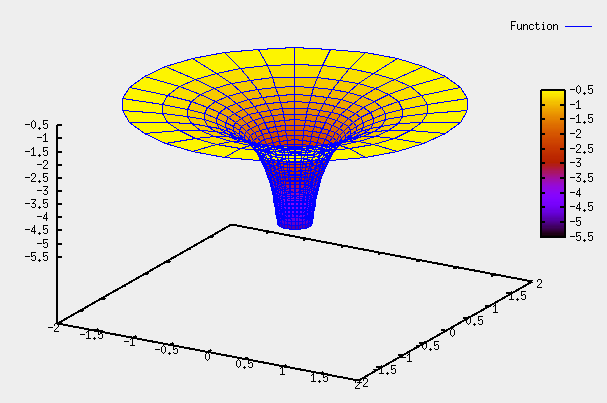
plot3d([cos(u)*(1/v),sin(u)*(1/v),-v],[u,0,2*%pi],[v,0.5,5], [gnuplot_pm3d,true]);
gnuplot_preamble
Legt Grafikoptionen für die Ausgabe (mit gnuplot) fest, z.B.:
plot3d([cos(u),sin(u),v],[u,0,4*%pi],[v,-5,5], ['grid,60,10], [gnuplot_preamble, "set terminal png; set out 'public_html/thema-mathematik/images/zylinderflaeche_04'"]);
Legt als Ausgabedatei eine Grafikdatei im PNG-Format, im angegebenen Pfad fest. Die Ausgabe von farbigen Grafiken wie im obigen Beispiel ist dabei nicht möglich.
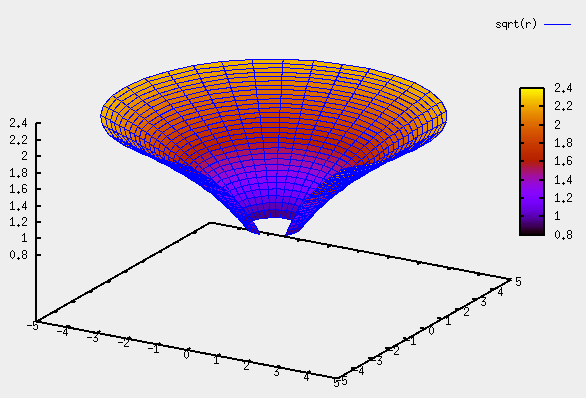
Polardarstellung
Die Darstellung von Rotationsflächen ist mit Hilfe der Polardarstellung recht einfach.
Beispiel: Rotation einer linearen Funktion
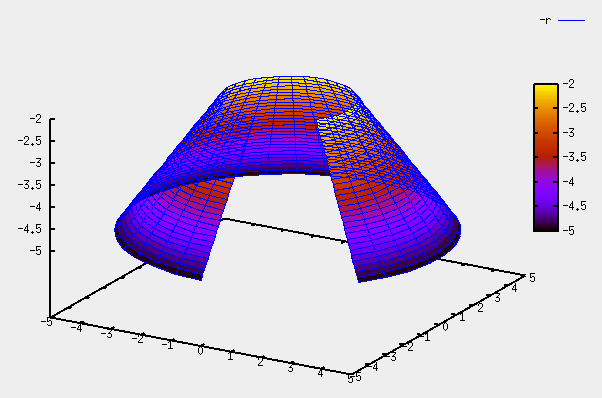
Beachte: Die lineare Funktion -r wird im Intervall [2,5] dargestellt. Eine Strecke rotiert und erzeugt den Mantel eines Kegelstumpfes.
Die Rotationsfläche wird im Intervall [-%pi/5, 3*%pi/2] dargestellt. Die Rotationsfläche wird nicht in einer vollen Umdrehung dargestellt, sondern erscheint „aufgeschnitten“
plot3d(-r,[r,2,5],[th,-%pi/5,3*%pi/2], ['transform_xy,polar_to_xy], [gnuplot_pm3d,true]);
Beispiel: Rotation der Sinuskurve
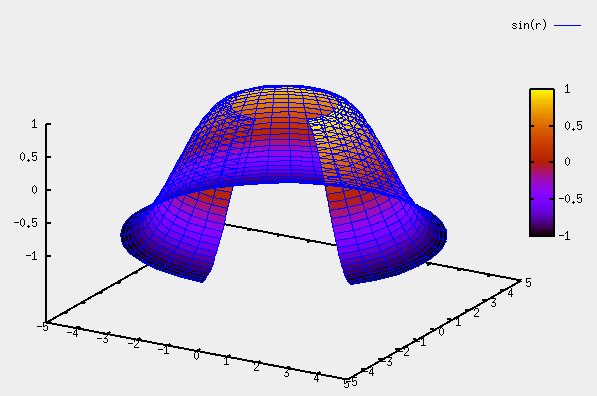
Beachte: Die Sinuskurve sin® wird im Intervall [%pi/2; 3*%pi/2] dargestellt. Dieses Stück der Sinuskurve rotiert und erzeugt die Rotationsfläche.
Die Rotationsfläche wird im Intervall [-%pi/5, 3*%pi/2] dargestellt. Die Rotationsfläche wird nicht in einer vollen Umdrehung dargestellt, sondern erscheint „aufgeschnitten“
plot3d(sin(r),[r,%pi/2,3*%pi/2],[th,-%pi/5,3*%pi/2], ['transform_xy,polar_to_xy], [gnuplot_pm3d,true]);
Weitere Beispiele:
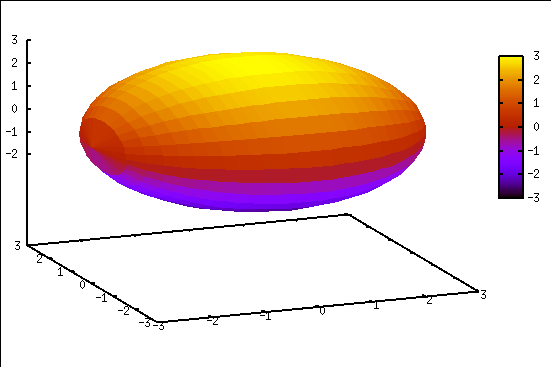
Rotation um x-Achse
Kugel
Beachte: Zuerst das Paket „draw“ laden!
load(draw);
Dann Funktion definieren, deren Graph um die x-Achse rotiert:
(%i37) f(x):=sqrt(9-x^2);
Mantelfläche (nach gnuplot) ausgeben:
(%i40) draw3d(surface_hide=true,enhanced3d=true,parametric_surface(x,-f(x)*sin(t),f(x)*cos(t),t,0,2*%pi,x,-3,3)); (%o40) [gr3d(parametric_surface)]
Anmerkung: Die Skalierung in Richtung der x-Achse kann durch die Angabe eines weiteren Darstellungsintervalls, z.B. x,-6,-6 beeinflusst werden.
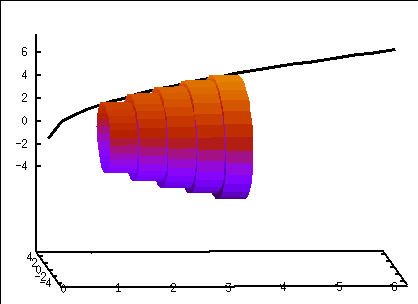
Rotationskörper durch Zylinderscheiben annähern:
(%i12) draw3d(surface_hide=true,enhanced3d=true,parametric_surface(x,-f(1)*sin(t),f(1)*cos(t),t,0,2*%pi,x,1,1.5), parametric_surface(x,-f(1.5)*sin(t),f(1.5)*cos(t),t,0,2*%pi,x,1.5,2), parametric_surface(x,-f(2)*sin(t),f(2)*cos(t),t,0,2*%pi,x,2,2.5), parametric_surface(x,-f(2.5)*sin(t),f(2.5)*cos(t),t,0,2*%pi,x,2.5,3), parametric_surface(x,-f(3)*sin(t),f(3)*cos(t),t,0,2*%pi,x,3,3.5),color=black,line_width=3,enhanced3d=false,parametric(x,0,f(x),x,0,2*%pi));
Weblinks
Zurück zu Maxima | Zurück zu Kurven und Flächen im Raum