Der Viertelkreis in Parameterdarstellung
x = 4 cos(α) y = 4 sin(α)
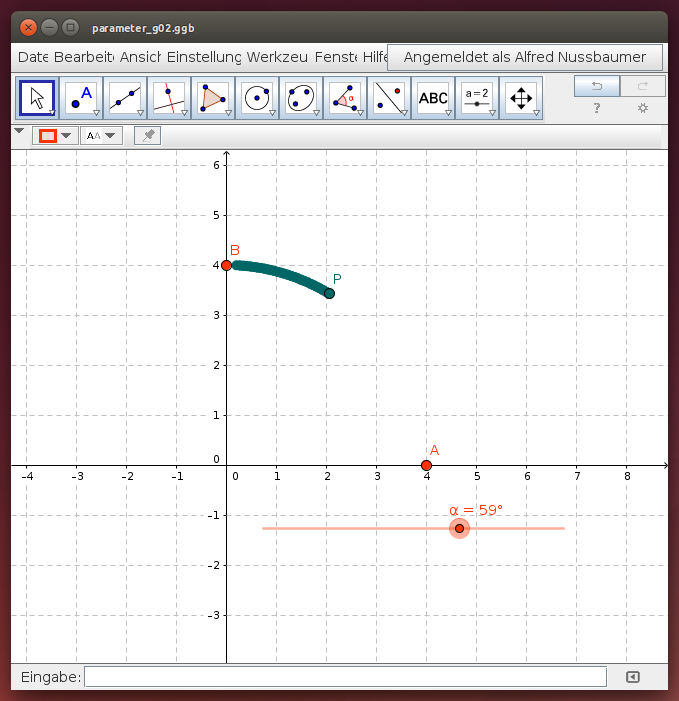
Wähle im folgenden GeoGebra-Applet die Position des Punktes P mit dem Schieberegler α. Die Spur des Punktes P stellt den Viertelkreis von A nach B dar:
(Hinweis: Mit <Strg>-F wird der Bildschirm neu aufgebaut)
Aufgaben:
- Überprüfe und begründe die Positionen des Punktes P für α = 0° und für α = 90°!
- Begründe, dass die Spur des Punktes P ein Viertelkreisbogen ist!
- Verändere die Positionen der Punkte A und B und untersuche, in welchem Intervall α alle Punkte des Viertelkreises ergibt!
- Ausblick: Wähle verschiedene Entfernungen der Punkte A und B vom Koordinatenursprung. Begründe, dass die Spur des Punktes P dann einen Ellipsenbogen beschreibt!
zurück zu Parametrisierte Kurven | Analytische Geometrie der Ebene