Inhaltsverzeichnis
Lernpfad Fraktale
(zu 
6, Folgen und Reihen, S. 71, S. 85, S. 88)
Bei diesem Lernpfad sammelst du Wissen zu einem faszinierenden, interdisziplinären Gebiet der Naturwissenschaften und Mathematik: Du untersuchst fraktale Strukturen, wie sie beispielsweise in der Natur, in der Technik und bei zahlreichen computergenerierten Grafiken vorkommen. Viele Ergebnisse lassen sich in ästhetisch ansprechenden Grafiken darstellen!
Fraktale Gebilde begegnen uns in der Natur sehr häufig. Wir untersuchen sie zum Beispiel in Zusammenhang mit geometrischen Reihen.
Geometrische Reihen
- Halbkreise: Immer kleiner werdende Halbkreisbögen werden so aneinander gefügt, dass eine (lange?) „Wellenlinie“ entsteht …
- Quadrate: Quadrate werden aneinander gefügt, wobei die Seitenlänge des folgenden Quadrats jeweils halbiert wird …
- Quadrate: Quadrate werden auf der Geraden y = x „aufgefädelt“, wobei die Seitenlänge des folgenden Quadrats jeweils halbiert wird …
Iterativ konstruierte Fraktale
Fraktale lassen sich durch wiederholte Anwendung der gleichen Konstruktionsvorschrift erzeugen. Folgende GeoGebra-Applets stellen solche Verfahren vor - öffne die Konstruktion durch einen Doppelklick auf das Applet und führe die Konstruktion fort!
- Die Kochinsel: Interpretieren wir das Innere der Schneeflockenkurve als zusammenhängende Fläche, so entsteht eine Insel. Wir untersuchen ihren Flächeninhalt und ihre Küstenlänge …
- Mit GeoGebra - Werkzeugen lassen sich selbstähnliche Figuren rasch konstruieren. Zwei solcher Werkzeuge stehen im Applet zur Selbstähnlichkeit zur Verfügung.
Die fraktale Dimension
Iterationen mit komplexen Zahlen
Wir iterieren komplexe Zahlen:
- Die Mandelbrotmenge - wir beobachten die Iteration
- Die Mandelbrotmenge mit GeoGebra erzeugen …
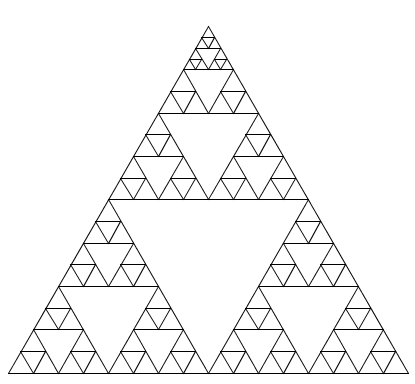
Chaos und Sierpinski-Dreieck
Online Fraktal-Generatoren
Lindenmayer-Systeme
Lindenmayer-Systeme (L-Systeme) erlauben eine mathematische Beschreibung von fraktalen Strukturen, die sich in der Natur beobachten lassen. Die Selbstähnlichkeit wird durch die rekursive Ersetzung von Abbildungsregeln erreicht.
Beispiel:
Das obige Bild wurde mit Mark Masse's L-System Applet (Universität Konstanz) durch folgende Ersetzungsregeln erzeugt:
Axiom: X
Ersetzungsregeln:
X=c007700[+X]F[+FX][-X]FX[+X][w(2)c660011-F]X,
X=c007700[+X]F[+FX][-X]FX[+X][w(2)c660011-F]X
Anfangswinkel: 270°, Rotationswinkel 47°
Hinweis: Der Farbwert wird mit einem vorangestellten „c“ festgelegt,
die Strichstärke durch w(..).
Aufgabe:
Erkunde L-Systeme mit Online-Generatoren:
- QuerKop (Stefan Beck)
- Mark Masse's L-System Applet (Universität Konstanz)
Ausblick
- Fraktalantennen finden Anwendung bei WLAN und Mobiltelefon (www.fractenna.com).
Zu Folgen und Reihen | Wachstumsmodelle | Komplexe Zahlen und algebraische Gleichungen
