(zu Lernpfad Fraktale, Lernpfad Komplexe Zahlen, Komplexe Zahlen und algebraische Gleichungen)

Iterierte Berechnungen mit komplexen Zahlen können überraschende Ergebnisse liefern. Für die Mandelbrotmenge untersuchen wir die Iteration

,

Liegt eine komplexe Zahl in der Nähe des Ursprungs der komplexen Zahlenebene, so ist zu erwarten, dass ihr Quadrat ebenfalls unweit des Ursprungs zu liegen kommt. Die Überraschung ergibt sich aus der fortwährenden Addition der ursprünglichen Zahl…

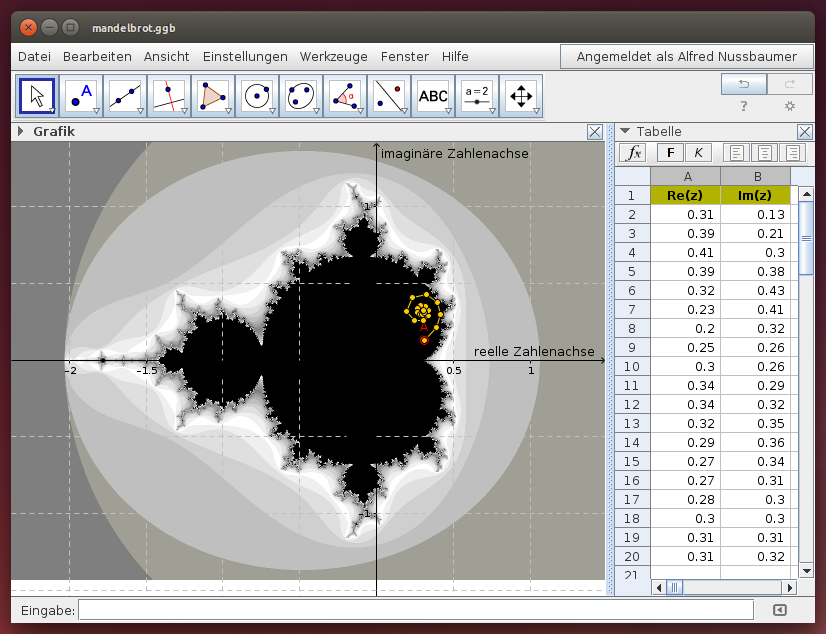
Im folgenden GeoGebra-Beispiel werden die ersten 20 Iterationen mit der Zahl c = A (die in der komplexen Zahlenebene als Punkt dargestellt wird) berechnet. Die Iterationsergebnisse sind ebenfalls als Punkte in der komplexen Zahlenebene sichtbar - um die Entwicklung der Iteration besser ablesen zu können, sind die Iterationsschritte durch Strecken verbunden.

Verschiebe den Punkt A über dem „Apfelmännchen“ und beobachte, wie sich die Iterationen jeweils entwickeln!

Download der GeoGebra-Datei

(Hintergrundbild erstellt mit Wacker Art Fractal Generator, www.wackerart.de/fractal.html)

• Untersuche, unter welchen Bedingungen sich die Folge der komplexen Zahlen „einrollt“, also konvergiert, und unter welchen Bedingungen sie divergiert!
• Vergleiche mit der Iteration z, z², z³, z⁴, … komplexer und reeller Zahlen (Beispiel 1, Beispiel 2, Beispiel 3, Beispiel 4, Beispiel 5)!
• Beschreibe den Zusammenhang mit Fraktalen (Lernpfad Fraktale)!

Zurück zu Lernpfad Fraktale | Lernpfad Komplexe Zahlen | Komplexe Zahlen und algebraische Gleichungen