Fortlaufende Potenzen komplexer Zahlen
Wir beobachten das Verhalten der Zahlenfolge z, z2, z3, z4, … unter der Bedingung, dass | z | = 1 gilt. Die Zahl z liegt in der Gauss'schen Zahlenebene somit auf dem Einheitskreis.
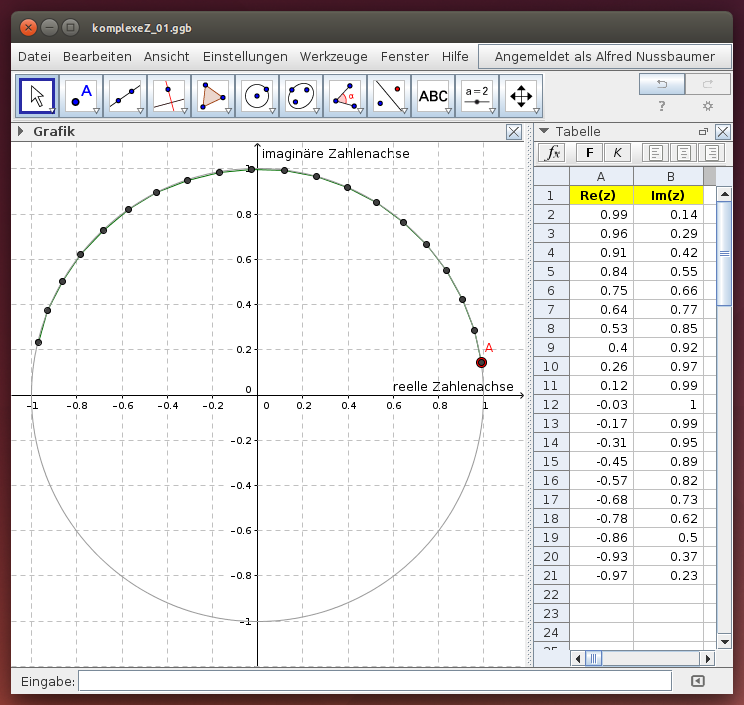
Wähle im folgenden GeoGebra-Beispiel den Startwert für z, indem du den roten Punkt A auf dem Einheitskreis verschiebst:
Aufgaben:
- Begründe: Die Zahlenfolge z, z2, z3, z4, … ist nicht konvergent.
- Gib den Betrag der Folgenglieder z, z2, z3, z4, … an!
- Vergleiche mit den fortlaufenden Potenzen reeller Zahlen: Welche Anfangswerte entsprechen den alternierenden reellen Zahlenfolgen? Gib Spezialfälle an!
Zurück zu Lernpfad Komplexe Zahlen | Komplexe Zahlen und algebraische Gleichungen | Fraktale